机器学习中的梯度下降与损失函数

梯度下降（Gradient Descent GD）简单来说就是一种寻找目标函数最小化的方法，它利用梯度信息，通过不断迭代调整参数来寻找合适的目标值。

什么是梯度？

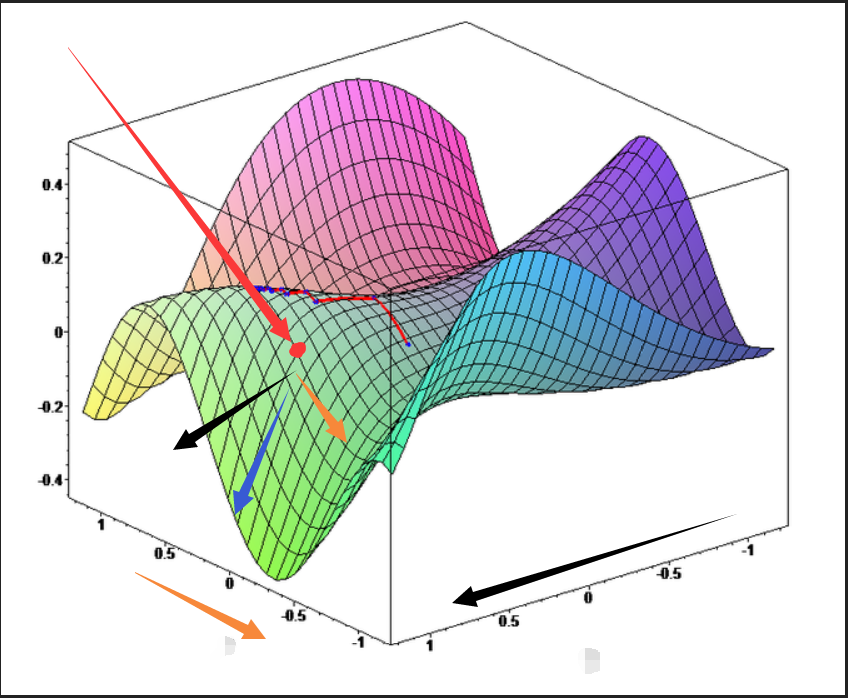
关于梯度的引入，可以分为四个概念：导数->偏导->方向导数->梯度
导数：当函数定义域和取值都在实数域中时，导数可以表示函数曲线上的切线斜率。

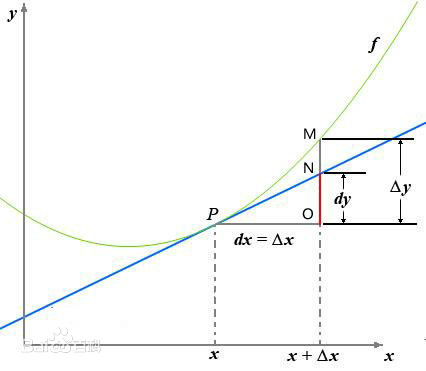
偏导数：偏导其实就是多元函数一个多变量的函数的偏导数是它关于其中一个变量的导数，而保持其他变量恒定。因为曲面上的每一点都有无穷多条切线，描述这种函数的导数相当困难。偏导数就是选择其中一条切线，并求出它的斜率 。几何意义是表示固定面上一点的切线斜率。
多元函数降维时候的变化，比如[二元函数]固定y，只让x单独变化，从而看成是关于x的[一元函数]的变化来研究。

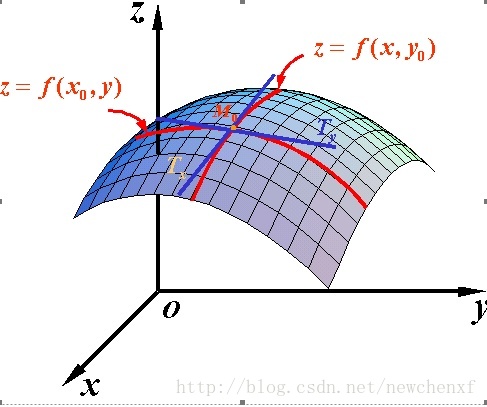
但是偏导数有一个缺点，就是只能表示多元函数沿[坐标轴]方向的变化率，但是很多时候要考虑多元函数沿任意方向的变化率，于是就有了方向导数。
方向导数：某个方向的导数，本质就是函数在A点上无数个切线的[斜率]的定义，每个切线都代表一个方向，每个方向都是有方向导数的。

梯度：梯度是一个矢量，在其方向上的方向导数最大，也就是函数在该点处沿着梯度的方向变化最快，变化率最大。

那么在机器学习中逐步逼近、迭代求解最优化时，经常会使用到梯度，沿着梯度向量的方向是函数增加的最快，更容易找到函数的最大值，反过来，沿着梯度向量相反的地方，梯度减少的最快，更容易找到最小值。

tips:其实“ 梯度”你 Ctr+H替换成“ 导数”就可以了，梯度就是目标函数的导数。

什么是梯度下降？

举个常见的例子：你站在山上某处，想要尽快下山，于是决定走一步算一步，也就是每走到一个位置时，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走，这样一直走下去，很可能走不到山脚，而是某个局部的山峰最低处。如下图所示：

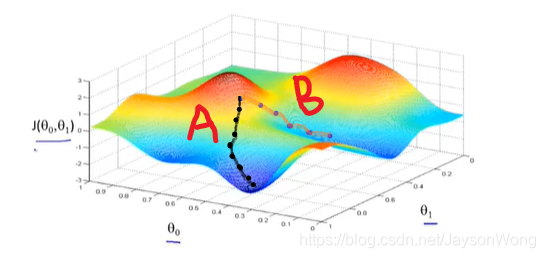
以上，我们可以总结一下：梯度下降法就是沿着梯度下降的方向求解极小值，沿着梯度上升的方向可以求得最大值，这种方法叫梯度上升。
从上图可以看到：受到起始点和目标函数特性的影响，梯度下降不一定找到的是全局最优解，可能只是局部最优解，那么什么时候能找到全局最优解呢？这个与损失函数有关，当损失函数是凸函数的话，可以找到全局最优。

梯度下降有什么用？

用问题一的解决方案，替换“梯度”为“导数”。问题变成了： 导数下降干嘛的？我暂时把答案写上稍后解释： 梯度下降就是用来求某个函数最小值时自变量对应取值。这个函数名字叫做损失函数（cost/loss function），直白点就是误差函数。一个算法不同参数会产生不同拟合曲线，也意味着有不同的误差。 损失函数就是一个自变量为算法的参数，函数值为误差值的函数。梯度下降就是找让误差值最小时候算法取的参数。（看到这里肯定也是一脸懵逼，马的好不容易知道梯度是啥现在又tmd多了个损失函数，不急看完损失函数是啥再回头看就懂了梯度下降干嘛的了）

什么是损失函数（误差函数）？

机器学习算法中 有一类算法就是产生一条曲线来拟合现有的数据，这样子就可以实现预测未来的数据，这个专业术语叫做回归（见到回归就替换成拟合就好了~^~）。 还有另外一种类似也是产生一条曲线，但是这个曲线时用来将点分隔成两块，实现分类，在这个曲线一侧为一类另外一侧算一类。 但是我怎么知道这个算法产生的拟合曲线效果好不好呢？这个东东叫做误差，预测值减去真实值最后取绝对值，没错就是这么简单粗暴~~
产生的拟合曲线并不是完全和现有的点重合，拟合曲线和真实值之间有一个误差。一个算法不同参数会产生不同拟合曲线，也意味着有不同的误差。 损失函数就是一个自变量为算法的参数，函数值为误差值的函数。梯度下降就是找让误差值最小时候这个算法对应的参数。（是不是突然感觉好像知道了梯度下降干嘛的了）

梯度下降中的重要概念

根据上述梯度下降的求解原理，我们需要了解如下几个梯度下降相关的重要概念：

• 步长（Learning rate）:每一步梯度下降时向目标方向前行的长度,用上面下山的例子，步长就是在当前这一步所在位置沿着最陡峭最易下山的位置走的那一步的长度。步长越长，在陡峭区域下降的越快，但在平缓区容易出现反复抖动而找不到最优点；步长越短越不易产生抖动，但是容易陷入局部最优解。
• 假设函数（hypothesis function）:在监督学习中为了拟合输入样本，而使用的假设函数，常用h()表示，对于线性回归模型，假设函数就是函数 $$ Y = W_0 + W_1X1 + W_2X2 + … + W_nX_n $$
• 损失函数（loss function）： 常用J()表示，为了[评估模型]的好坏，通常用损失函数来度量拟合的程度。损失函数最小化，意味着拟合程度最好，对应的模型参数即为最优参数。每个机器学习模型都有一个损失函数，学习的目的就是将损失函数最小化。

算法步骤

梯度下降的具体算法实现过程是：

• 确定模型的假设函数和损失函数
• 相关参数的初始化，包括：参数、算法终止距离和步长
• 确定当前位置损失函数的梯度
• 用步长乘以梯度，得到当前位置下降的距离
• 确定是否所有参数梯度下降的距离都小于算法终止距离，如果小于则算法终止，否则进行下一步
• 更新所有参数，更新完毕转到步骤1

梯度下降面临的问题：

梯度下降会遇到所有最优化问题中常见的两个问题：局部最小值和鞍点。

局部最小值

这是梯度下降法最常遇到的一个问题，当一个函数存在多个局部最小值，很可能梯度下降法只是找到其中的一个局部最小值而停止。
怎么避免呢？
下山的例子中，我们看到初始值不同，获得的最小值可能不同，所以规避局部最小值最简单的方法可以多次用不同的初始值执行算法，选择损失函数最小的初始值。

鞍点

鞍点是最优化问题中常遇到的一个现象，鞍点的数学含义是：目标函数在此点的梯度为0，但从该点出发的一个方向存在函数极大值点，而另一个方向是函数的极小值点。

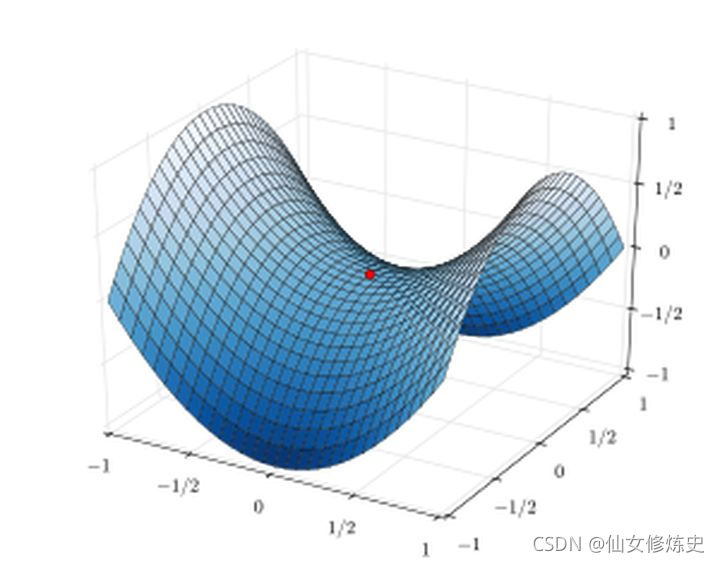
在高度非凸空间中，存在大量的鞍点，这使得梯度下降法有时会失灵，虽然不是极小值，但是看起来确是收敛的。

常见的梯度下降法

批量梯度下降（Batch Gradient Descent BGD）

上面所介绍的算法其实就是批量梯度下降。需要首先计算所有数据上的损失值，然后再进行梯度下降，具体的操作步骤是：遍历全部数据集算一次损失函数，然后算函数对各个参数的梯度，更新梯度。这种方法每更新一次参数，都要把数据集里的所有样本计算一遍，计算量大，计算速度慢，不支持在线学习。

随机梯度下降（Stochastic Gradient Descent SGD）

不使用全量的样本来计算梯度，而使用单一样本来近似估计梯度，可以极大地减少计算量，提高计算效率。具体的操作步骤是：每次从训练集中随机选择一个样本，计算其对应的损失和梯度，进行参数更新，反复迭代。
这种方式在数据规模比较大时可以减少计算复杂度，从概率意义上来说的单个样本的梯度是对整个数据集合梯度的无偏估计，但是它存在着一定的不确定性，因此收敛速率比批梯度下降得更慢。

小批量梯度下降（Mini-batch Gradient Descent）

为了克服上面两种方法的缺点，采用的一种折中手段：将数据分为若干批次，按批次更新参数，每一批次中的一组数据共同决定了本次梯度的方向，下降起来就不容易跑偏，减少了随机性，另一方面，因为批的样本数比整个数据集少了很多，计算量也不是很大。

每次使用多个样本来估计梯度，这样可以减少不确定性，提高收敛速率，其中每次迭代选取的样本数量称为批大小（batch size）。

梯度下降法和其他无约束优化算法的比较

在机器学习中的无约束优化算法，除了梯度下降以外，还有前面提到的最小二乘法，此外还有牛顿法和拟牛顿法。
梯度下降法和最小二乘法相比，梯度下降法需要选择步长，而最小二乘法不需要。梯度下降法是迭代求解，最小二乘法是计算解析解。如果样本量不算很大，且存在解析解，最小二乘法比起梯度下降法要有优势，计算速度很快。但是如果样本量很大，用最小二乘法由于需要求一个超级大的逆矩阵，这时就很难或者很慢才能求解解析解了，使用迭代的梯度下降法比较有优势。
梯度下降法和牛顿法/拟牛顿法相比，两者都是迭代求解，不过梯度下降法是梯度求解，而牛顿法/拟牛顿法是用二阶的海森矩阵的逆矩阵或伪逆矩阵求解。相对而言，使用牛顿法/拟牛顿法收敛更快。但是每次迭代的时间比梯度下降法长。