辐射度量学为计算机图形学提供物理正确的光照计算基础,通过定义辐射能量、通量、立体角和辐射强度等物理量,使渲染结果从“看起来像”转变为“物理正确”,是通往路径追踪等高级渲染技术的基石。
先导
“光到底是什么?”
这是为了回答一个你在写 Blinn-Phong 模型代码时可能产生的终极疑问:“我的光照强度设为 10,但这个 10 到底是什么单位?是 10 个灯泡?还是 10 个太阳?”
如果没有这套物理系统,Whitted-style 光线追踪的结果永远只是“看起来像”,而不是“物理正确” 。
为什么要学辐射度量学 (Radiometry)?
辐射度量学是一套精确测量电磁辐射(包括光)空间属性的系统。它引入了一系列物理量(如辐射通量、强度、辐照度、辐射亮度),让我们能够以物理正确的方式进行光照计算 。
在此之前的渲染器就像是在画画,颜色深浅全凭感觉调参数(比如
float intensity = 10.0)。 学完这部分后,你的渲染器将变成一台照相机。每一个像素的颜色值,都对应着真实物理世界中打到底片上的能量数值。这是通往路径追踪 (Path Tracing) 的必经之路 。
基础概念
能量与通量
**辐射能量 (Radiant Energy, $Q$)**定义为:电磁辐射的能量。其单位是焦耳 (Joule, $J$) 。
Tip 说人话:就像水池里蓄的总水量。但在图形学中我们很少直接用它,因为光通常是持续不断的。
**辐射通量 / 功率 (Radiant Flux / Power, $\Phi$)**定义为:单位时间内发射、反射、传输或接收的能量 。其公式表达为:
$$ \Phi \equiv \frac{dQ}{dt} $$其单位为:瓦特 (Watt, $W$) 或 流明 (Lumen, $lm$)
Note 上述两个概念可以通俗理解为:光子流。想象光是水流。能量 ($Q$) 是这一盆水有多少。通量 ($\Phi$) 是水龙头的流速。单位时间流出来的光子越多,这盏灯就越“亮”。比如一个 60W 的灯泡,这个“瓦数”描述的就是它的 Flux(虽然电功率和光功率有转换效率问题,但概念类似)。
立体角 (Solid Angle,$\Omega$)
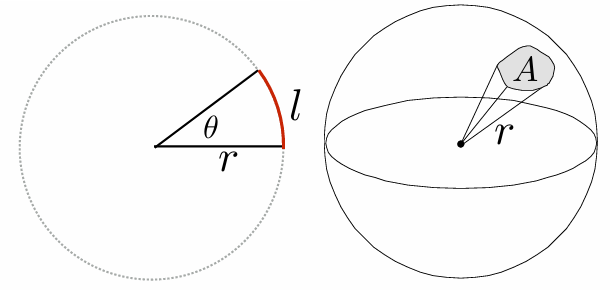
在定义更复杂的物理量之前,我们需要先复习一下几何。因为光线是在三维空间中向四面八方发射的,我们不能只用平面角度。
平面角度回顾:弧长除以半径,$\theta = l/r$。圆的总角度是 $2\pi$ 。立体角定义:球面上的面积除以半径的平方。其公式为:
$$ \Omega = \frac{A}{r^2} $$其单位为:球面度 (steradian, $sr$)。带入整个球面值计算可以得到:球的表面积是 $4\pi r^2$,所以整个球面的立体角是 $4\pi$ 。
微分立体角
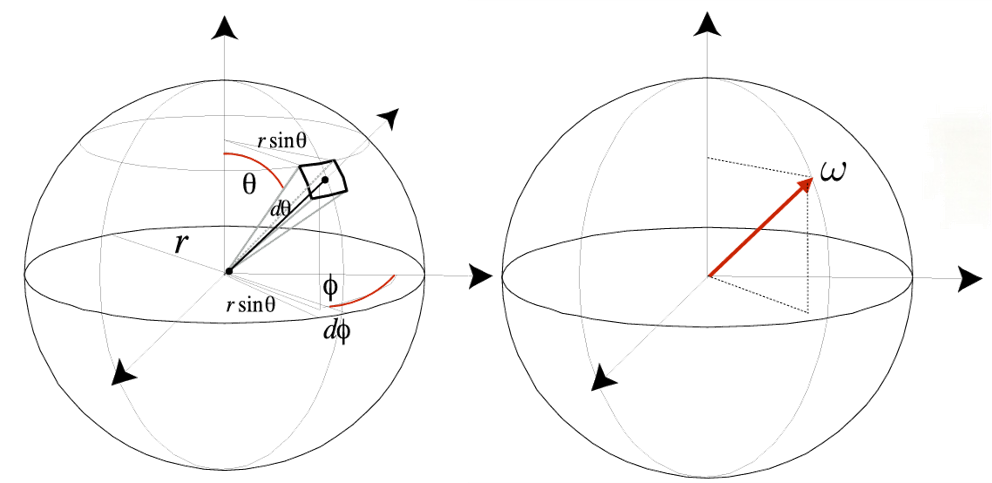
在球坐标系下:$d\omega = \sin\theta d\theta d\phi$ 。这就好比在球面上切了一块极其微小的长方形面积,用来积分光线方向。
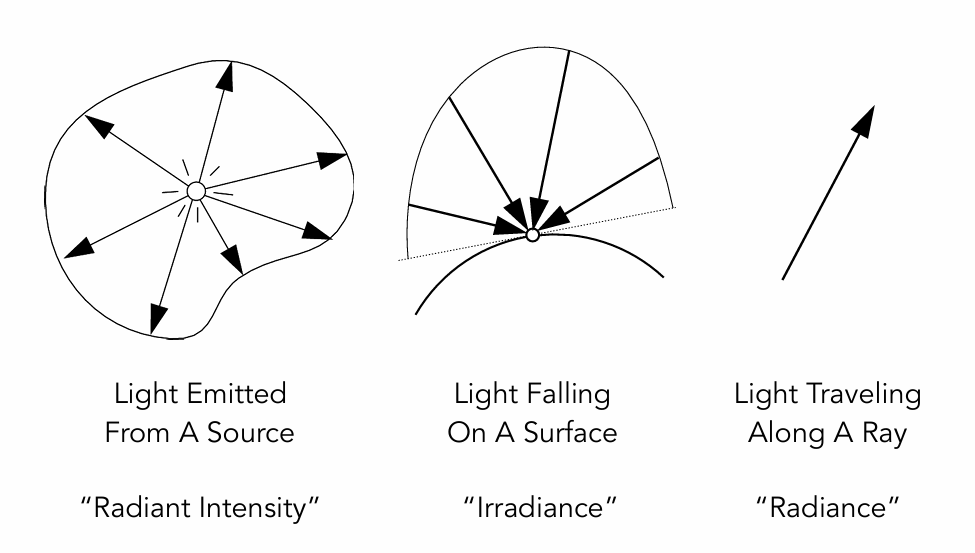
辐射强度 (Radiant Intensity, $I$)
这是本节课介绍的第三个核心概念,专门用来描述点光源。
辐射强度 (Radiant Intensity)定义为:点光源在单位立体角内发射的功率 。其公式:
$$ I(\omega) \equiv \frac{d\Phi}{d\omega} $$单位:坎德拉 (Candela, $cd$),即 $W/sr$ 或 $lm/sr$ 。
Note 这个概念可以通俗理解为“激光笔” vs “灯泡”。假设你有两个光源,Flux(总功率)都是 10W。灯泡:光线向四面八方散开($4\pi$),每个方向分到的能量很少,所以不刺眼。激光笔:把这 10W 的能量集中在一个极小的立体角方向发射出去。虽然它们的总能量流速(Flux)一样,但激光笔在那个特定方向上的Intensity(强度) 极高,甚至能亮瞎眼。
各向同性点光源 (Isotropic Point Source):如果一个点光源向所有方向发射的光都是一样的(比如理想的灯泡),则其总通量 可以表示为:
$$ \Phi = \int I d\omega = I \times 4\pi $$反之,已知总通量求平均的方向强度则可以表达为:
$$ I = \frac{\Phi}{4\pi} $$举个生活的栗子解释一下:

包装上写着:Brightness 815 Lumens。这就是 Flux ($\Phi$),表示这灯泡每秒发出的总光能。
它的辐射强度 (Intensity) 是多少?计算得:假设它向四面八方均匀发光(各向同性)。球面立体角 = $4\pi \approx 12.57$。强度 $I = 815 / 12.57 \approx 65$ Candelas。
辐照度 (Irradiance, $E$)
定义:单位面积上接收到的辐射通量(功率)。单位:$W/m^2$ 或 Lux。可以用公式表示为:
$$ E(x) \equiv \frac{d\Phi(x)}{dA} $$Lambert’s Cosine Law:接收到的能量与光线入射角的余弦值 ($\cos \theta$) 成正比 。
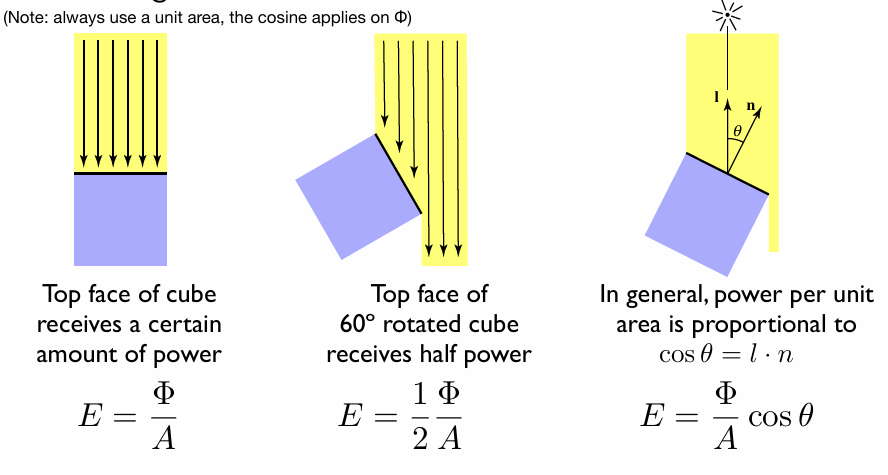
这里的概念可以通俗的做一个**“太阳能板”类比**,想象你手里拿一块太阳能板(单位面积 $dA$)。Irradiance 就是这块板子一共充进去多少电。
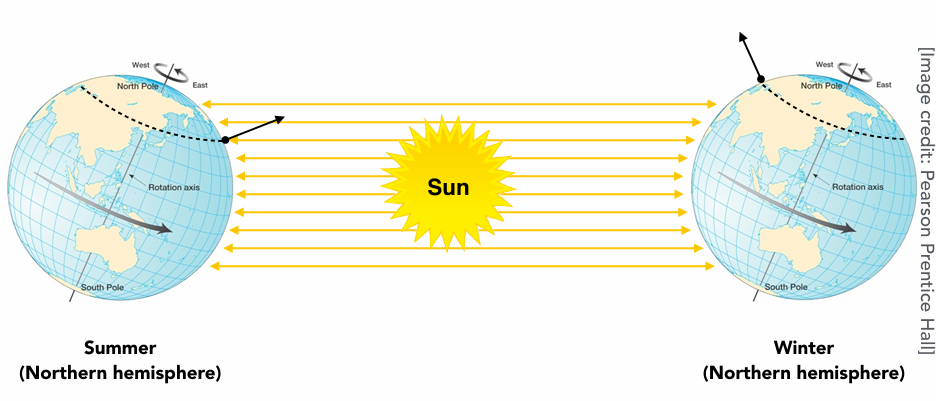
为什么有 Cosine Law?
如果太阳直射($\theta=0$),光束垂直打在板子上,接收能量最大。如果板子倾斜了($\theta$ 变大),同样粗细的一束光,现在要铺在更大的面积上,能量密度就稀释了。这解释了为什么地球有四季:冬天太阳斜射,单位面积接收的热量(Irradiance)变少了 。
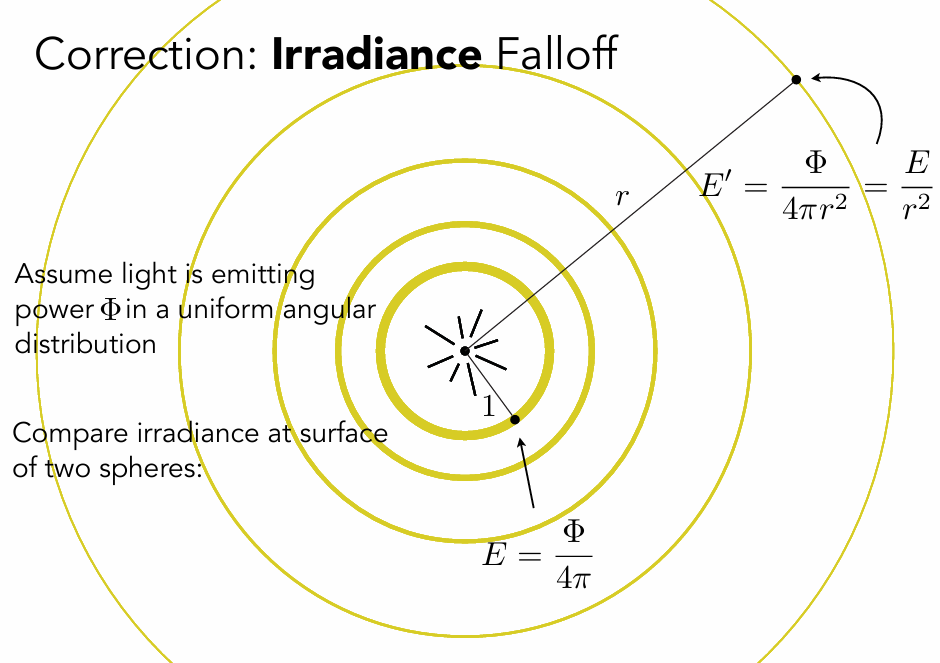
光线能量衰减:离灯越远越暗,因为光能量铺在了更大的球面上,我们用小学二年级学过的球的表面积公式就可以算出:Irradiance 随距离平方衰减 ($1/r^2$) 。
辐射亮度 (Radiance, $L$)
辐射亮度 (Radiance, $L$)定义为:单位立体角、单位投影面积 (Projected Unit Area) 上的功率 。可以用公式表示为
$$ L(p, \omega) \equiv \frac{d^2\Phi(p, \omega)}{d\omega dA \cos \theta} $$
Note Radiance 是光线追踪中,光线 (Ray) 身上携带的那个量。渲染算出来的像素颜色,本质上就是 Radiance 。
这个物理概念仍然可以做一个通俗**“细水管”类比**,
Irradiance 是整个地面($dA$)被淋湿的总水量。它不关心水是从哪来的,只关心收到了多少。Radiance 是某一根特定的细水管($d\omega$方向),喷到地面投影区域上的水量。
为什么要除以 $\cos \theta$(投影面积)?这就好比你从侧面看电脑屏幕,虽然屏幕实际面积没变,但你看到的“有效面积”变扁了。Radiance 描述的是你眼里看到的亮度,所以必须基于你看到的那个“投影面积”来算。
Note 一句话总结:
光打在物体上,我们要算 Irradiance(接收了多少能量)。光从物体反射到相机里,我们要算 Radiance(看起来有多亮)。
BRDF ($f_r$)
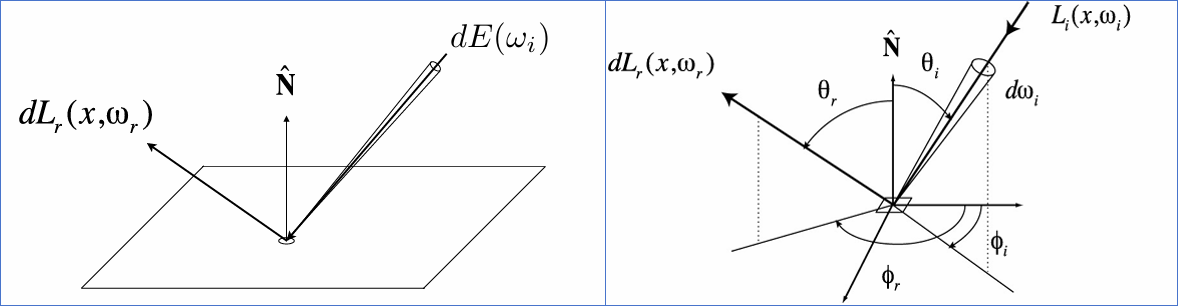
BRDF是材质的灵魂,决定了高光、粗糙度、颜色吸收等视觉属性。其全称是:双向反射分布函数 (Bidirectional Reflectance Distribution Function)。定义材质的光学特性,描述入射光如何被表面反射为出射光。即:入射的微分 Irradiance ($dE$) 转化为了多少出射的微分 Radiance ($dL_r$) 。可以用公式表述为:
$$ f_r(\omega_i \to \omega_r) = \frac{dL_r(\omega_r)}{L_i(\omega_i) \cos \theta_i d\omega_i} $$
Note BRDF 是光线与表面碰撞时的“反弹规则”。光线打到物体上,就像一把球扔到地上。BRDF 就是地面的反弹规则。
镜面 (Mirror):球扔下来,BRDF 规定它们必须整整齐齐地向一个方向弹走。漫反射 (Diffuse):球扔下来,BRDF 规定它们要向四面八方随机乱弹。深色物体:BRDF 规定“这一把球扔下来,我吃掉 90%,只弹走 10%”。
渲染方程 (The Rendering Equation)
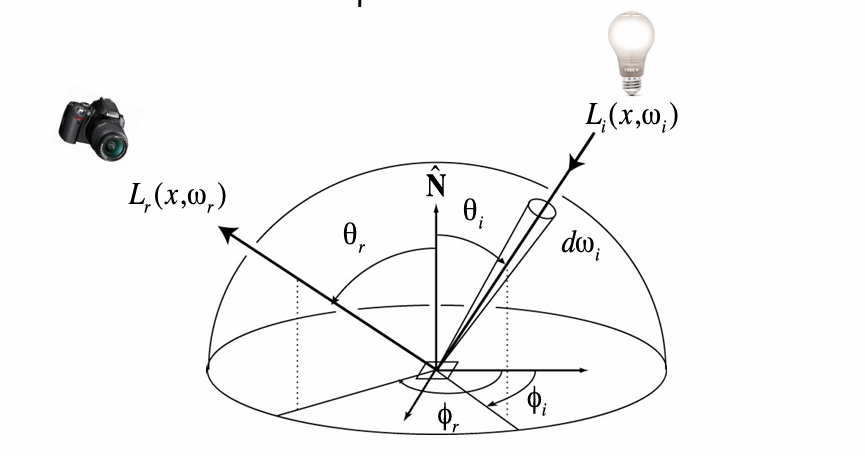
基于以上提到的概念,整个光线的轨迹就可以得到一个的终极方程:
$$ L_o(p, \omega_o) = L_e(p, \omega_o) + \int_{\Omega+} L_i(p, \omega_i) f_r(p, \omega_i, \omega_o) (n \cdot \omega_i) d\omega_i $$$L_o$ (出射光):我想算的像素颜色。$L_e$ (自发光):如果物体自己发光(比如灯泡),这一项不为0 。$\int_{\Omega+}$ (积分):我们需要把半球面上所有四面八方来的光都加起来。$L_i$ (入射光):从某个方向飞来的光。$f_r$ (BRDF):材质决定反射多少。$n \cdot \omega_i$ (Cosine项):就是 $\cos \theta$,接收能量的衰减 。
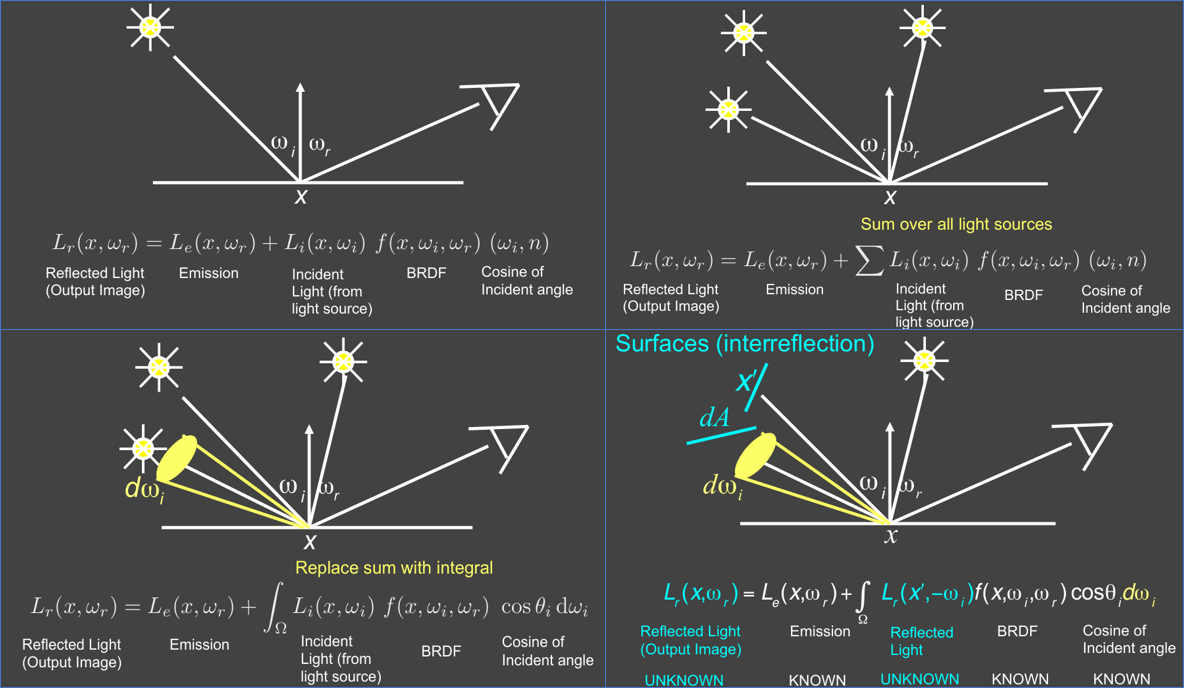
渲染方程描述的计算步骤是:
先看我自己发不发光?($L_e$)
如果不发光,通过 BRDF 收集周围的光。
麻烦来了(递归求解):我想知道点 A 的颜色,必须知道点 B 射给 A 的光 ($L_i$),但点 B 射出的光,又是点 B 的反射光 ($L_o$),点 B 的反射光,又取决于点 C 射给 B 的光… 这意味着光线在场景里无限反弹!
全局光照 (Global Illumination)
现在用数学级数来理解光线的反弹,把渲染方程简写为线性算子形式:
$$ L = E + KL $$把上面公式通过二项式定理展开,可以得到级数:
$$ L = E + KE + K^2E + K^3E + ... $$这是一场**“光的接力赛”**
$E$:光源本身(你是灯泡,你直接亮),$KE$ (Direct Illumination):光 $\to$ 物体 $\to$ 眼睛。这是传统光栅化做的(直接光照)。**$K^2E$ (Indirect, 1-bounce)**则是:光 $\to$ 墙 $\to$ 物体 $\to$ 眼睛。比如红墙把旁边的白球映红了(Color Bleeding)。$K^nE$:光弹了 n 次才进眼睛。
全局光照 (GI):就是要把这无穷无尽的项都加起来!光线追踪之所以拟真能力非常强,就是因为它在尝试计算这些后面复杂的项 。

如上图所示,在计算初次光线反射时,仅包含光源的直接照射,因此建筑天花板及墙面背光侧因无光照而完全暗沉,缺乏细节。而当计算中引入第一次光线折射后,光线得以在场景中反弹,间接照亮了原本不可见的区域,使天花板及背光墙面开始显现结构细节。进一步观察可发现,当折射计算从第八次增加至第十六次时,画面差异已非常细微,肉眼难以直接察觉,表明结果已趋于收敛。
Tip 门中部的玻璃灯具效果则更为复杂,其透射光的显现需计算至第四次折射时才被捕捉。这是由于从太阳发出的光线需先穿过透明灯体,经折射后抵达相机,完整路径至少涉及两次透射过程。
Note 值得注意的是,多次折射并未导致画面整体亮度异常增加——因为每帧计算中光线初始能量固定,遵循能量守恒,每次反射或折射均伴随能量衰减,后续折射对最终画面的贡献已逐渐减弱,不会产生类似相机长曝光般的过曝现象。