计算机图形学是研究计算机中图形表示、生成、处理和显示的交叉学科,其核心内容包括图形表示、生成、处理与显示,并与计算机视觉、图像处理等学科紧密关联。学习图形学需要掌握线性代数基础,如向量的点乘、叉乘及矩阵运算。
基本概念

计算机图形学是什么?
计算机图形学(Computer Graphics)是研究如何在计算机中表示、生成、处理和显示图形的学科。它结合了数学、物理学、计算机科学和艺术等多个领域的知识,致力于解决如何在计算机上创建和操作视觉内容的问题,其最直观的用途包括如下四个方面。
- 图形表示:研究如何在计算机中表示2D和3D图形对象
- 图形生成:如何从模型数据生成可视图像
- 图形处理:对已有图形进行变换、编辑和优化
- 图形显示:如何将生成的图形高效地显示在输出设备上
图形学(CG)与其他学科的关系
- 计算机视觉(CV):图形学是"从模型到图像",计算机视觉是"从图像到模型"
- 图像处理:图形学绘制(渲染)图像,图像处理修改已有图像
- 计算几何:提供图形学所需的几何算法
- 人机交互:图形学为HCI提供可视化界面
为什么要学图形学?
因为图形学很酷!

线性代数基础
向量的点乘(Dot Product)
两个向量的点乘结果是一个标量
$$ \vec{a} \cdot \vec{b} = \|\vec{a}\| \|\vec{b}\| \cos\theta $$几何意义:
- 点乘 > 0:两向量方向基本相同(夹角 < 90°)
- 点乘 = 0:两向量垂直(夹角 = 90°)
- 点乘 < 0:两向量方向基本相反(夹角 > 90°)
向量的叉乘(Cross Product)
两个向量的叉乘结果是一个新向量
性质:
- 结果向量同时垂直于原始两个向量
- 方向由右手定则决定:
- 右手四指从a向b握紧,拇指指向即为a×b方向
- 大小等于两向量构成的平行四边形面积
矩阵形式表示:
a × b = A* b 其中A*是a的反对称矩阵:
$$ \begin{bmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix} $$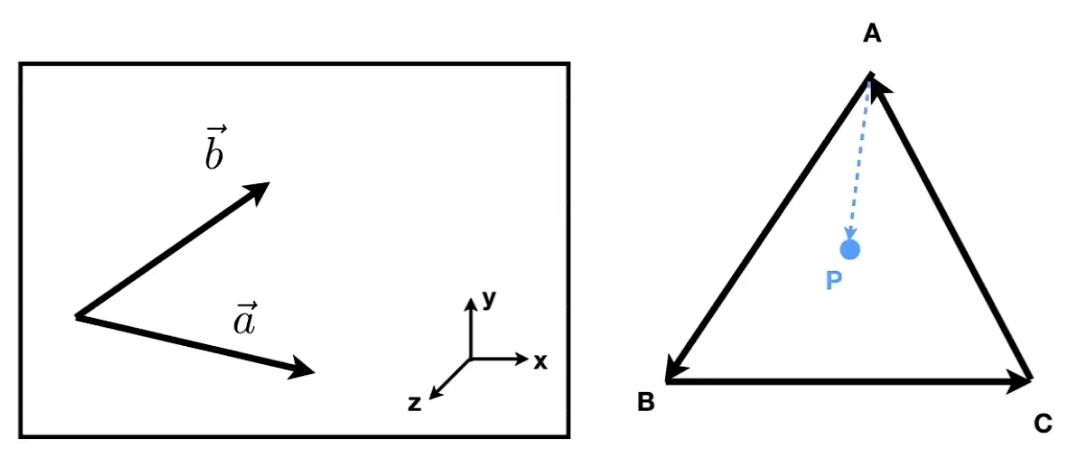
判断向量左右关系:
- a×b与z轴同向 → b在a左侧
- a×b与z轴反向 → b在a右侧
判断点是否在三角形内(光栅化关键算法):
- 对三角形ABC和点P,检查: AB×AP > 0 且 BC×BP > 0 且 CA×CP > 0
- 全部满足则P在三角形内
矩阵运算
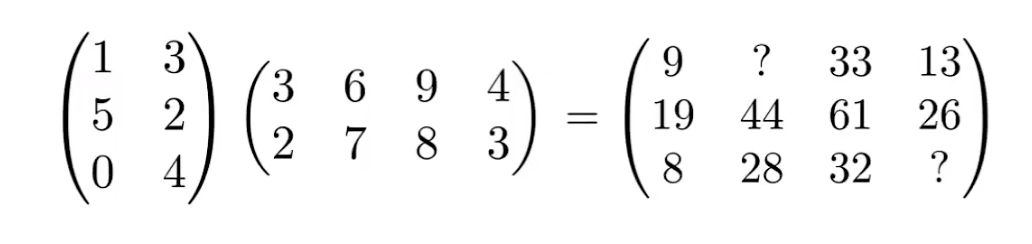
矩阵乘法:
- 要求:(M×N)矩阵 × (N×P)矩阵 = (M×P)矩阵
- 计算方法:结果矩阵的第(i,j)元素 = 第一个矩阵第i行与第二个矩阵第j列的点积
特殊矩阵:
- 单位矩阵:对角线为1,其余为0
- 逆矩阵:A⁻¹满足A⁻¹A = AA⁻¹ = I
- 转置矩阵:行列互换
矩阵与向量:
- 点乘的矩阵形式:a·b = aᵀb
- 叉乘的矩阵形式:a×b = A* b(A*为a的反对称矩阵)