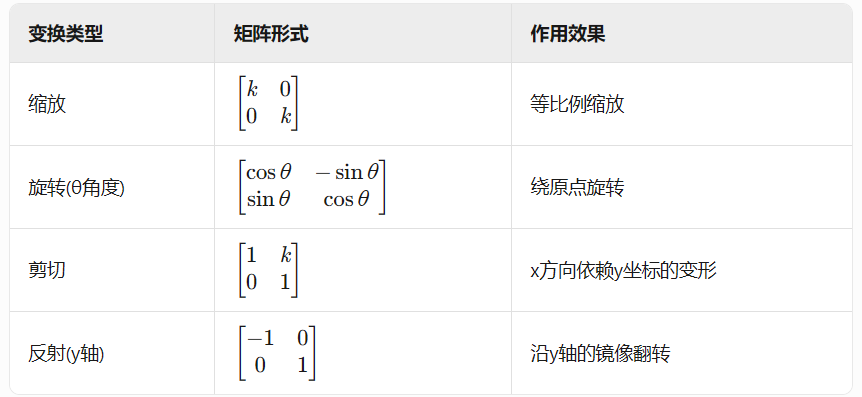
计算机图形学中的基本变换包括缩放、镜像、错切和旋转,每种变换都可通过特定的数学矩阵来描述物体在二维空间中的位置、大小和方向变化。
变换Transformation是计算机图形学中的基础概念,用于描述和操作物体在二维或三维空间中的位置、方向和大小。
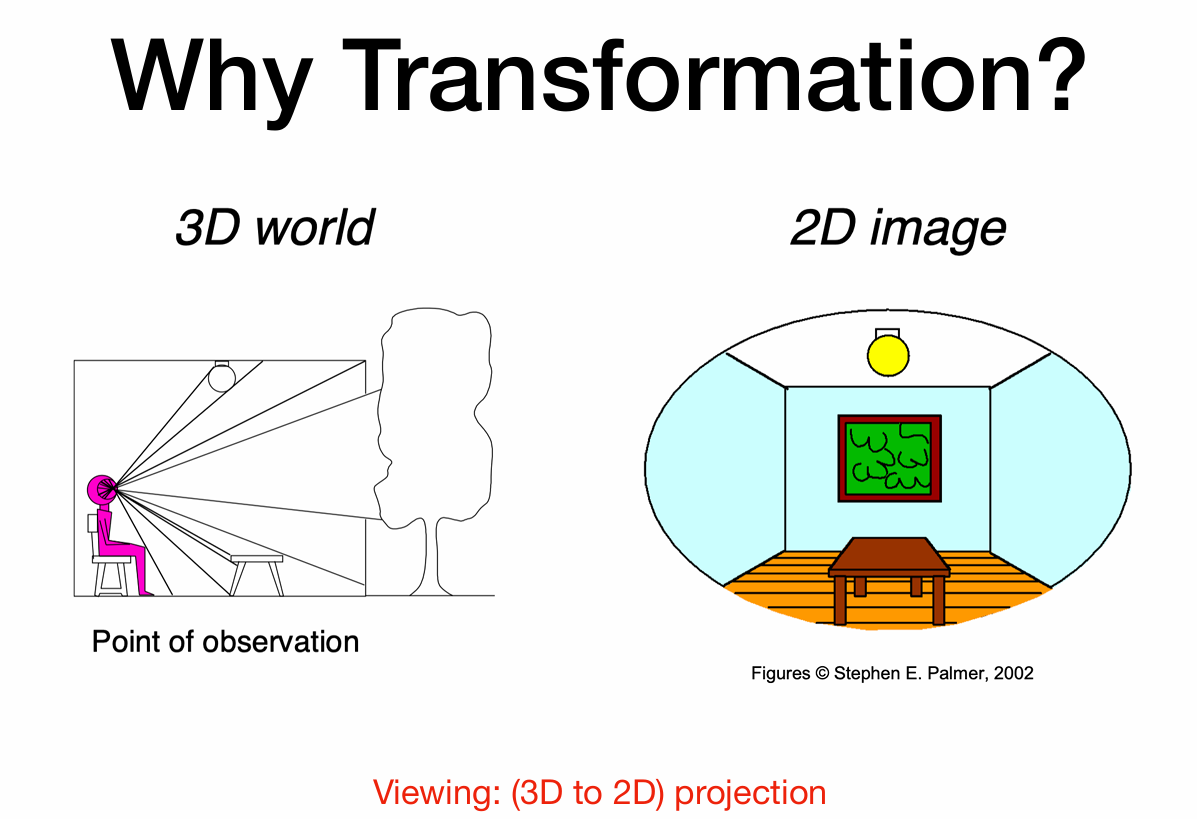
基本变换类型
缩放变换(Scale)
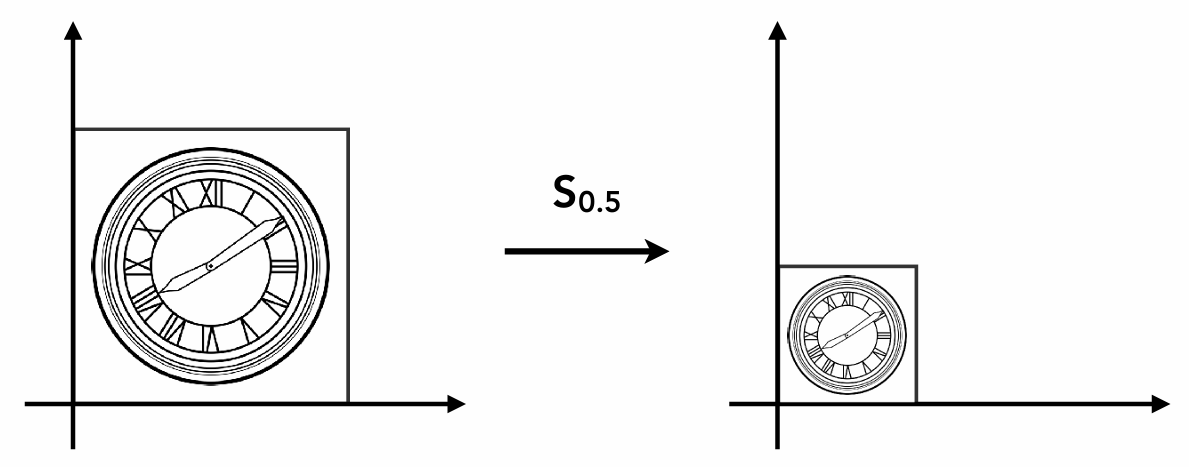
如图所示的坐标轴内物体缩放,其数学变换公式为: $$ \begin{aligned} x' &= s \cdot x \\ y' &= s \cdot y \end{aligned} $$ 矩阵格式表述为: $$ \begin{bmatrix} x’ \ y' \end{bmatrix}
\begin{bmatrix} s & 0 \ 0 & s \end{bmatrix} \begin{bmatrix} x \ y \end{bmatrix} $$ 而以此推广为非对称缩放变化:
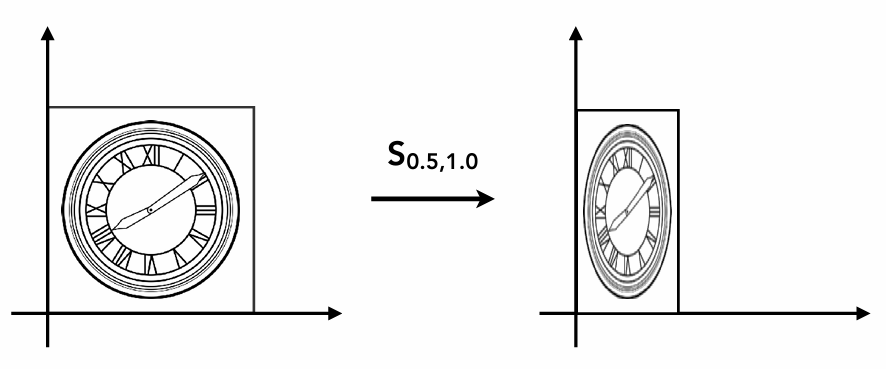
此处的矩阵表述如下所示: $$ S = \begin{bmatrix} s_x & 0 \ 0 & s_y \end{bmatrix}
\begin{bmatrix} 0.5 & 0 \ 0 & 1.0 \end{bmatrix} $$
$$ \left[\begin{array}{l} x^{\prime} \ y^{\prime} \end{array}\right]
\left[\begin{array}{cc} s_{x} & 0 \ 0 & s_{y} \end{array}\right] \left[\begin{array}{l} x \ y \end{array}\right] $$
镜像变换(Reflection)
如下图所示,对于镜像变换,也是直接修改x,y的值就好
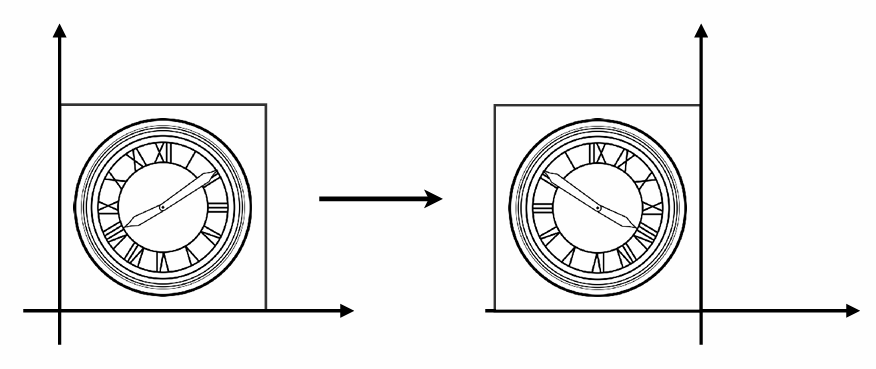
其数学变换与矩阵表达如下所示:
$$ \begin{cases} x' = -x \\ y' = y \end{cases} $$$$ \left[\begin{array}{l} x^{\prime} \ y^{\prime} \end{array}\right]
\left[\begin{array}{cc} -1 & 0 \ 0 & 1 \end{array}\right] \left[\begin{array}{l} x \ y \end{array}\right] $$
错切变换(Shear)
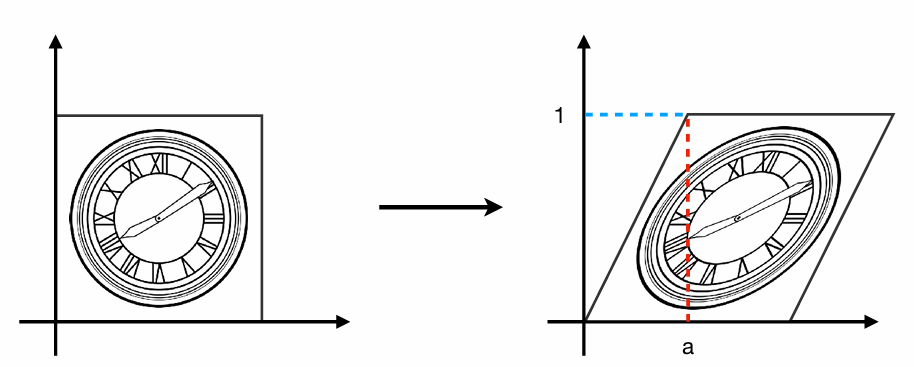
如上图所示:变换后的图形每个点的y坐标都没变,对于左上角的点来说变化应该是0+a,对于右上角的点来说变化应该是1+a,对于左边中间的点来说变化应该是0+a/2,所以每个点的变化应该是: $$ x' = x + a y $$ 其矩阵表达为: $$ \left[\begin{array}{l} x^{\prime} \ y^{\prime} \end{array}\right]
\left[\begin{array}{ll} 1 & a \ 0 & 1 \end{array}\right] \left[\begin{array}{l} x \ y \end{array}\right] $$
旋转变换(Rotation)
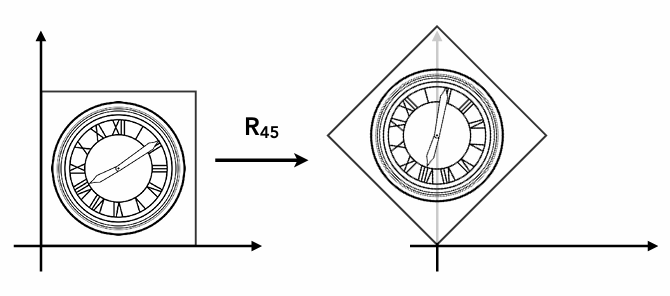
我们假设旋转角为θ,以原来的原点、x轴点、y轴点为例进行观察
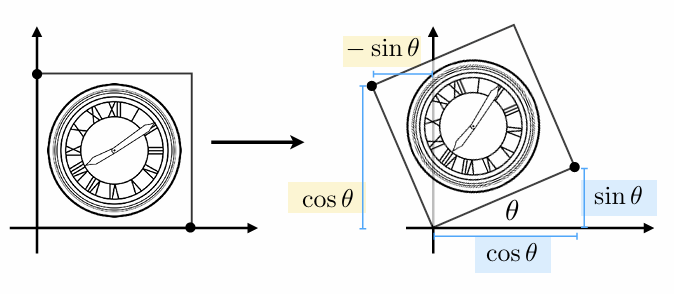
原本的x轴点从(x,0)变为( x* cosθ, x* sinθ),而原本的y轴点由(0,y)变为(-y*sinθ,y * cosθ). $$ \begin{cases} x' = a x + b y \\ y' = c x + d y \end{cases} $$ 这里我们假设原本的坐标向量(x,y)乘以一个旋转矩阵向量R从而得到了现在的坐标向量(x’,y’) $$ \left[\begin{array}{c} x’ \ y' \end{array}\right]
\left[\begin{array}{cc} a & b \ c & d \end{array}\right] \left[\begin{array}{c} x \ y \end{array}\right] $$ 其公式推导如下:
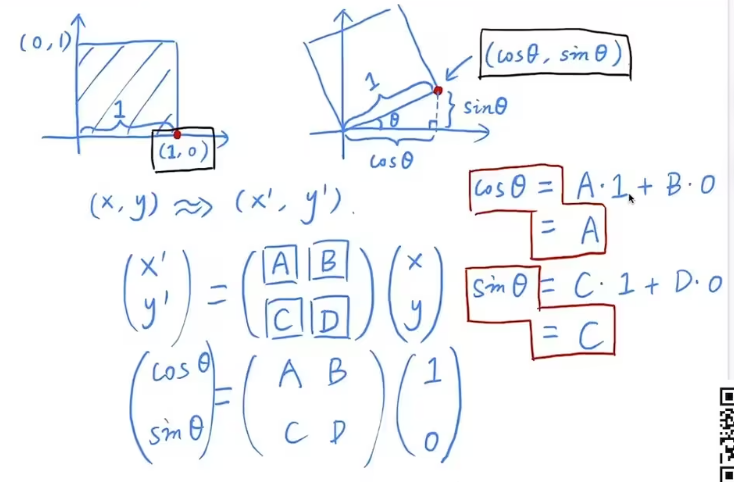
得到的推导结果:
$$ R_\theta = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} $$$$ \mathbf{x}' = \mathbf{M}\mathbf{x} \quad \text{其中} \quad \mathbf{M} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} $$
Tip 以上的变换统称线性变换,线性变换在矩阵中的定义是可以通过一次乘法直接得到结果的运算
平移变换(Translation)
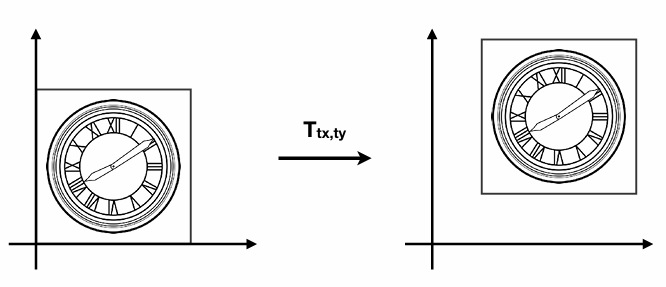
而平移变换看似简单,却无法用线性变换矩阵来表示,其数学表达如下: $$ \begin{cases} x' = x + t_x \\ y' = y + t_y \end{cases} $$ 其写为矩阵表达如下: $$ \left[\begin{array}{l} x^{\prime} \ y^{\prime} \end{array}\right]
\left[\begin{array}{ll} a & b \ c & d \end{array}\right] \left[\begin{array}{l} x \ y \end{array}\right] + \left[\begin{array}{l} t_{x} \ t_{y} \end{array}\right] $$ 人类总是犯懒的,最想做的事就是一步到位而不要这么多繁琐的操作,为了解决这个问题,引入齐次坐标的概念(所谓齐次坐标暂且可以先理解为加了一个坐标轴,用于将平移变换统一到我们的一般变换中),齐次后的矩阵表达式如下所示: $$ \left(\begin{array}{c} x^{\prime} \ y^{\prime} \ w^{\prime} \end{array}\right)
\left(\begin{array}{ccc} 1 & 0 & t_{x} \ 0 & 1 & t_{y} \ 0 & 0 & 1 \end{array}\right) \cdot \left(\begin{array}{l} x \ y \ 1 \end{array}\right)
\left(\begin{array}{c} x + t_{x} \ y + t_{y} \ 1 \end{array}\right) $$ 而之前的所有变换操作在齐次坐标下仍然可用:
Scale:
$$ \mathbf{S}(s_x, s_y) = \begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{pmatrix} $$Rotation:
$$ \mathbf{R}(\alpha) = \begin{pmatrix} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{pmatrix} $$Translation:
$$ \mathbf{T}(t_x, t_y) = \begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix} $$$$ \mathbf{M} = \mathbf{T}(t_x,t_y) \cdot \mathbf{R}(\alpha) \cdot \mathbf{S}(s_x,s_y) $$
Caution 当图像进行多个变换时,其复合表达式应该从右往左写,并且乘法交换率在矩阵中并不适用
如上式,表示的是某图像先缩放,然后旋转,最后后再平移。
3D变换
3D变换相对于2D变换来说只是多增加了一个维度,可由2D变换举一反三得来:
Scale:
$$ \mathbf{S}(s_x, s_y, s_z) = \left(\begin{array}{cccc} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) $$Translation:
$$ \mathbf{T}(t_x, t_y, t_z) = \left(\begin{array}{cccc} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{array}\right) $$3D旋转
3D旋转与2D旋转也基本一直,观察如下矩阵表示可以感受其几何意义:绕X轴旋转则x相关坐标无变化,所以x除对角线外的元素均为0,其余两个轴同理.
$$ \begin{array}{c} \mathbf{R}_{x}(\alpha)=\begin{pmatrix} 1 &0&0&0\\ 0 &\cos\alpha &-\sin\alpha &0\\ 0 &\sin\alpha &\cos\alpha &0\\ 0 &0&0&1 \end{pmatrix}\\ \mathbf{R}_{y}(\alpha)=\begin{pmatrix} \cos\alpha &0&\sin\alpha &0\\ 0 &1&0&0\\ -\sin\alpha &0&\cos\alpha &0\\ 0 &0&0&1 \end{pmatrix}\\ \mathbf{R}_{z}(\alpha)=\begin{pmatrix} \cos\alpha &-\sin\alpha &0&0\\ \sin\alpha &\cos\alpha &0&0\\ 0 &0&1&0\\ 0 &0&0&1 \end{pmatrix} \end{array} $$而绕y轴旋转有一点特殊,他在旋转之外进行了一个转置,这样做的原因是源于向量的叉乘:
$$ \begin{aligned} \mathbf{X} \times \mathbf{Y} &= \mathbf{Z} \\ \mathbf{Y} \times \mathbf{Z} &= \mathbf{X} \\ \mathbf{X} \times \mathbf{Z} &= -\mathbf{Y} \end{aligned} $$罗德里格斯旋转公式
观测变换(Viewing transformation)
视图/相机变换(View/Camera transformation)
图形学的最终目的是为了将三维中的物体渲染成二维里的图像,在现实生活中如何照一张照片?
找个好地方摆pose(Model变换),把相机放个好角度(View变换),按快门(投影Projection变换)。简称MVP🤭
视图View变换–如何摆放相机的角度,决定相机的位置,决定相机看向的方向,决定相机头朝上的方向。
考虑到我们要实现下面一种情况:一个无限大的场景中,相机和要拍摄的物体随意移动,只要相机对于某物体的相对变换(位置、朝向、缩放)相同,那么在相机拍摄出的画面中,该物体永远相同(不考虑光照)。
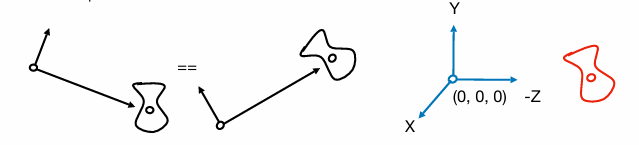
为了简化计算,一般将相机的位置永远规定在(0,0,0),并且其朝向永远和-Z轴相同,视为一个计算机图形学中的约定。
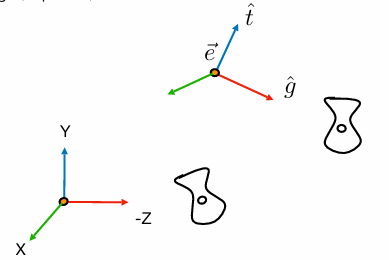
如上图所示,要把摄像机归到原点分三步
1.平移摄像机至(0,0,0)对原本的坐标点做平移变换
$$ T_{\text{view}} = \begin{bmatrix} 1 & 0 & 0 & -x_{e} \\ 0 & 1 & 0 & -y_{e} \\ 0 & 0 & 1 & -z_{e} \\ 0 & 0 & 0 & 1 \end{bmatrix} $$2.将相机lookat的方向旋转到-Z,旋转相机头朝上的方向到Y
$$ R_{\text{view}} = \begin{bmatrix} x_{\hat{g} \times \hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & 0 \\ x_{\hat{t}} & y_{\hat{t}} & z_{\hat{t}} & 0 \\ x_{-\hat{g}} & y_{-\hat{g}} & z_{-\hat{g}} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} $$3.得到变换矩阵
$$ M_{\text{view}} = R_{\text{view}} \cdot T_{\text{view}} = \begin{bmatrix} x_{\hat{g} \times \hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & -\vec{e} \cdot (\hat{g} \times \hat{t}) \\ x_{\hat{t}} & y_{\hat{t}} & z_{\hat{t}} & -\vec{e} \cdot \hat{t} \\ x_{-\hat{g}} & y_{-\hat{g}} & z_{-\hat{g}} & \vec{e} \cdot \hat{g} \\ 0 & 0 & 0 & 1 \end{bmatrix} $$$$ \text{(其中 } \vec{e} = (x_e, y_e, z_e) \text{ 是相机位置)} $$将Mview应用到相机,相机归零,同时也需要将Mview应用到其他所有物体,让物体和相机的相对位置保持不变
投影变换
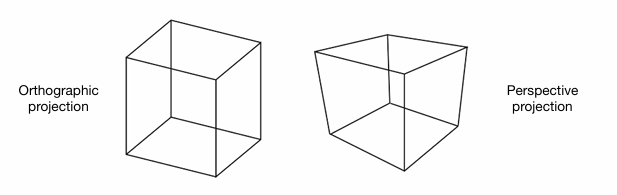
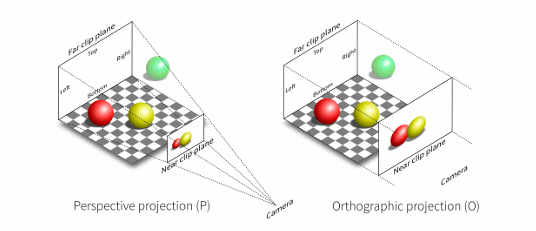
投影变换分为两种,一种是正交投影,一种是透视投影。其最核心的区别在于:透视投影会造成一个“近大远小”的现象,用一个梗来解释就是“道理我都懂,但是鸽子为什么这么大”🙂

Note 在现代游戏开发中,很多2D游戏是使用3D引擎去做的开发,然而其视图仍然能保持2D的感觉,使用的投影方式就正交投影。
正交投影
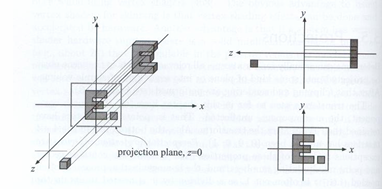
如上图所示,我们延续之前相机坐标归于原点的思想,可以得到下面的思维链条:
先将相机归零,并lookat -Z轴,直接把Z轴坐标舍弃,就能得到物体在xy平面上的投影,把得到的图像平移并且缩放到[-1,1]²中,方便之后的计算。
但在计算机图形学的实际过程中,有着更简化的计算方式,如下图所示
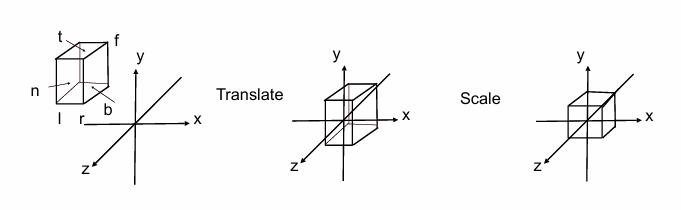
视口是个(l,r)(b,t)(f,n)的长方体,想让他变成[-1,1]³中只需要先将立方体的中心平移到原点,再将立方体缩放到[-1,1]³中
$$ M_{\text{ortho}} = \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{bmatrix} $$透视投影
透视投影是使用最广泛的投影方法,也是人眼的成像方式。
传统的欧式几何是在同一平面内生效的法则,对于不同平面就会造成照片中近大远小的情况
对于一个使用透视投影的绘制,应该怎样进行呢,如下图所示:
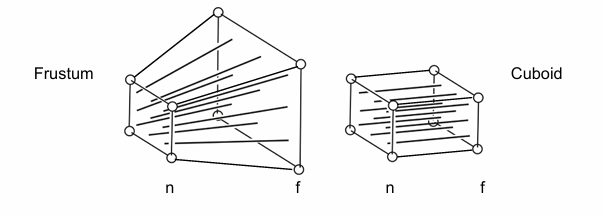
老师的方法是,先将Frustum远平面及远平面到近平面之间的所有平面挤压到近平面大小,变成Cuboid的样子,然后做一次正交投影。
怎样做挤压?
对于除近平面外的任意一个点,通过挤压后该点的高度y要变成和近平面一样的y’,从侧面看Frustum的话,如下图,可以形成两个相似三角形,即可得出y‘=(n/z)y,同理x’=(n/z)x。
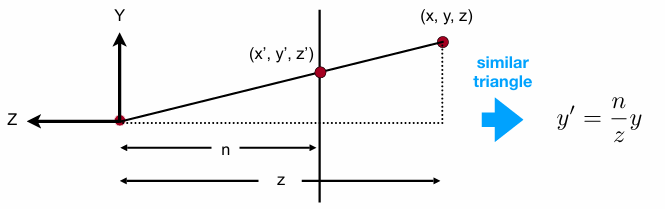
可以得到以下数学表达: $$ \begin{aligned} x' &= \frac{n}{z} x \\ y' &= \frac{n}{z} y \quad \text{(similar to } x') \end{aligned} $$ 将其表示为齐次坐标的形式: $$ \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} \Rightarrow \begin{pmatrix} nx/z \\ ny/z \\ \text{unknown} \\ 1 \end{pmatrix} \xrightarrow{\text{mult. }z} \begin{pmatrix} nx \\ ny \\ \text{still unknown} \\ z \end{pmatrix} $$ 现在我们对于投影的变换(挤压部分)有如下表达: $$ M_{\text{persp}\rightarrow\text{ortho}}^{(4\times4)} \begin{pmatrix} x \ y \ z \ 1 \end{pmatrix}
\begin{pmatrix} nx \ ny \ \text{unknown} \ z \end{pmatrix}
$$ 显而易见可以推理出M的部分值 $$M_{\text{persp}\rightarrow\text{ortho}} =
\begin{pmatrix}
n & 0 & 0 & 0 \
0 & n & 0 & 0 \
? & ? & ? & ? \
0 & 0 & 1 & 0
\end{pmatrix}
$$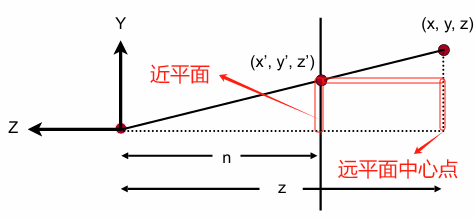
想补全这个矩阵,需要用到两条已知的性质,1是近平面的点坐标(x,y,z)都不会发生变化。2是远平面的点z的值不会发生变化(因为我们采用的方法是先压缩后正交)。
代入第一条性质(z值代为n) $$ \begin{pmatrix} x \ y \ n \ 1 \end{pmatrix} \Rightarrow \begin{pmatrix} x \ y \ n \ 1 \end{pmatrix}
\begin{pmatrix} n x \ n y \ n^{2} \ n \end{pmatrix} $$ 显然发现第三行的计算结果n方与x,y均无关系,故设第三行为 (0,0,*A*,*B*),则其满足 $$ \begin{pmatrix} 0 & 0 & A & B \end{pmatrix} \begin{pmatrix} x \ y \ n \ 1 \end{pmatrix} = n^2 $$ 将其展开推导: $$ An + B = n^{2} $$ 显然该式有无穷多解,现在结合上面第二条性质的特殊点--即远平面上的中心点压缩后仍然是原来的位置,我们设其坐标为(0,0,f),带入数学表达式,并写为统一格式。 $$ \begin{pmatrix} 0 \ 0 \ f \ 1 \end{pmatrix} \Rightarrow \begin{pmatrix} 0 \ 0 \ f \ 1 \end{pmatrix}
\begin{pmatrix} 0 \ 0 \ f^2 \ f \end{pmatrix}
$$ 展开得到: $$Af + B = f^{2}
$$ 联立两式解得: $$\begin{cases} An + B = n^{2} \ Af + B = f^{2} \end{cases} \quad \longrightarrow \quad \begin{cases} A = n + f \ B = -nf \end{cases}
$$ 至此解得了完整的压缩变换矩阵: $$M_{\text{persp}\rightarrow\text{ortho}} = \begin{pmatrix} n & 0 & 0 & 0 \ 0 & n & 0 & 0 \ 0 & 0 & n+f & -nf \ 0 & 0 & 1 & 0 \end{pmatrix}
$$ 对压缩结果再进行一步正交投影即可得到最终结果 $$M_{\text{persp}} = M_{\text{ortho}} \cdot M_{\text{persp}\rightarrow\text{ortho}} $$