动画通过连续图像产生运动感,其发展从手绘到数字时代。关键帧动画是基础技术,通过定义关键姿态并由计算机插值生成中间帧,数学本质是参数空间的插值过程。
动画概念
动画概述与历史
动画的本质是“赋予生命”,通俗来说就是通过随时间变化的场景模型,输出一系列连续图像,利用人眼的视觉暂留产生运动感 ,基于对人眼感知的能力,动画的帧数一般为以下的标准:
帧率标准:电影通常为 24 fps,一般视频为 30 fps,而虚拟现实(VR)则需要高达 90 fps 来保证流畅度 。

一些重要动画的发展史:
- 早期尝试:公元前 3200 年伊朗的陶器彩绘被认为是最早的动画原型 ;1831 年出现了诡盘(Phenakistoscope) 。
- 电影诞生:1878 年埃德沃德·迈布里奇拍摄的《萨莉·加德纳》是第一部电影,最初用于科学研究 。
- 手绘巅峰:1937 年迪士尼推出了首部长篇手绘动画《白雪公主与七个小矮人》 。
- 数字时代:1963 年 Ivan Sutherland 的 Sketchpad 开启了数字计算机生成动画的先河 ;1995 年《玩具总动员》成为首部全 CG 长篇电影 。
关键帧动画 (Keyframe Animation)
这是最传统也是最基础的动画技术 。关键帧动画的核心在于将动画序列分解为由核心动作组成的“关键点” 。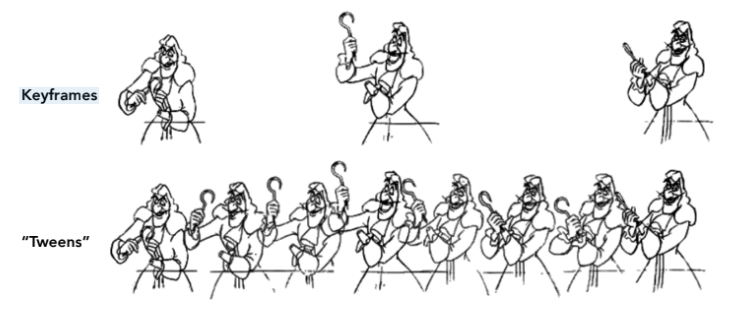
关键帧 (Keyframes):由资深动画师(Lead Animator)绘制,定义了动作在特定时间点的最核心、最具代表性的姿态 。
“补间” (Tweens):是指填充在两个关键帧之间的中间帧 。
角色分配:在传统动画中,中间帧通常由助理动画师完成;而在现代计算机动画中,这一任务主要由计算机通过算法自动生成 。
Tip 这种关键帧打点加上计算机混合的方式其实仍然很常见,记得我小时候就经常上电脑课玩flash,自己做点小动画,PPT的动画一般也是规定几个关键帧,有然后使用某个曲线插值生成的。
数学本质:参数空间插值
在计算机图形学中,关键帧动画被视为在参数空间内的插值过程 。
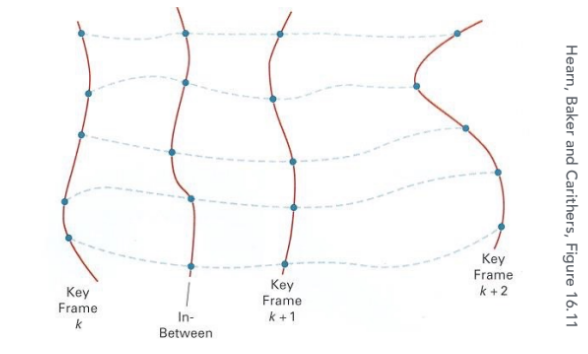
可以将动画中的每一帧看作一个包含多个参数(如位置、旋转角度、缩放比例等)的向量 。随时间变化的本质是将场景模型表示为时间的函数 $f(t)$ 。插值过程就是给定时间 $k$ 的参数状态和时间 $k+1$ 的参数状态,计算机通过数学函数计算出两者之间任意时间点的状态 。
如何让动作看起来自然、平滑,取决于使用的插值算法 。与之前学过的光栅化插值类似,也介绍几种经典的插值算法(实则是已经被基本淘汰的老古董)。
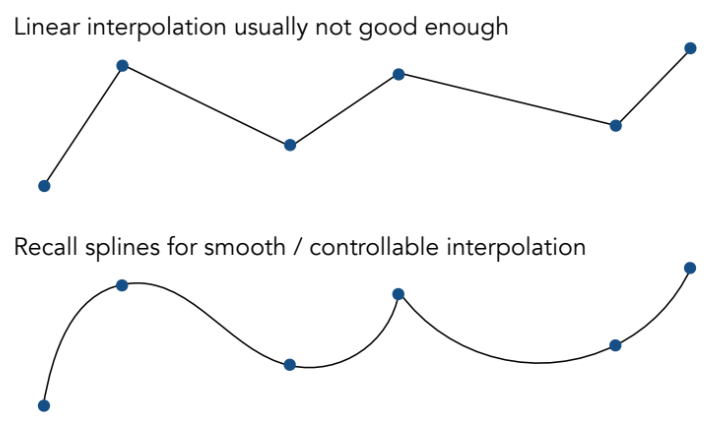
线性插值 (Linear Interpolation):这是最简单的方法,但通常效果并不理想 。线性插值会导致动作在关键帧处出现生硬的转折,缺乏物理上的真实感(例如忽略了加速度的影响) 。
样条线插值 (Splines):为了获得平滑且可控的动画效果,通常会使用样条线技术(如贝塞尔曲线或B样条)进行插值 。样条线可以确保参数在随时间变化时具有连续性,从而产生更流畅、自然的运动曲线 。
虽然关键帧动画提供了极高的艺术控制力,但也存在一些短板:
艺术性主导:动画的美学问题往往比技术问题更重要 。
制作成本:即便有计算机辅助,设置复杂的关键帧和调整插值曲线对于动画师来说依然是一项耗时且具有挑战性的工作 。
Tip 简单的线条很难模拟复杂的动画,做出来的效果也一眼假,所以引入了物理模拟动画:
物理模拟 (Physical Simulation)

在计算机图形学中,物理模拟的本质是数值仿真(Numerical Simulation) 。如果你想让一件衣服、一根头发或者一块果冻动起来,手动为成千上万个顶点打关键帧是不现实的 。我们需要一套逻辑,让物体能根据物理定律“自我演化”。**质点弹簧系统(Mass Spring System)**就是实现这一目标最直观、最经典的建模方法 。
牛二定律
先复习以下小学二年级学过的牛二定律:
$$ F = ma $$F (Force):作用在物体上的力 。m (Mass):物体的质量 。a (Acceleration):物体的加速度 。
通过已知的力 $F$ 和质量 $m$,可以求得加速度 $a$。通过加速度对时间积分,可以求得物体的速度和位置 :
$$ x^{t+\Delta t} = x^{t} + \Delta t v^{t} + \frac{1}{2}(\Delta t)^{2}a^{t} $$质点弹簧系统 (Mass Spring System)
如何构建一个“像样”的弹簧?
为了让多个质点连接成一个整体,我们需要一种“力”来维持它们之间的相对位置。这就是弹簧(Spring)。
**理想弹簧(连接与拉力)**假设有两个质点 $a$ 和 $b$,最简单的想法是:它们离得越远,拉力越大。
$$ f_{a \rightarrow b} = k_s (b - a) $$这符合胡克定律(Hooke’s Law),通过系数 $k_s$(劲度系数)控制材质的硬度 ,但是这种弹簧倾向于让长度变为 0 。如果没有外力,物体会瞬间坍缩成一个点。
引入静止长度(维持形状)为了让物体有固定的形状,我们需要给弹簧一个静止长度(Rest Length) $l$ 。
$$ f_{a \rightarrow b} = k_S \frac{b - a}{\|b - a\|}(\|b - a\| - l) $$只有当实际距离 $\|b-a\|$ 与 $l$ 不相等时,才会产生力。这让物体有了“恢复原状”的能力。但是此时这个系统一旦动起来,能量不会损失,会永远震荡下去 。
引入阻尼(模拟能量损耗)现实中的物体会停下来是因为有能量损耗。我们需要加入阻尼(Damping) 。
为什么不能简单地减慢所有速度?
如果你用 $f = -k_d v$,物体在空中飞行时也会变慢,这看起来像在胶水里运动 。更聪明的做法是:只针对弹簧内部的相对运动进行阻尼 。物体在整体平移或旋转时不会受阻,但内部的震动会迅速平息,这才是自然的质感 。
如何用弹簧织出一块布?
当你把这些质点连接成网格时,你会发现简单的横竖连接根本不像布料。
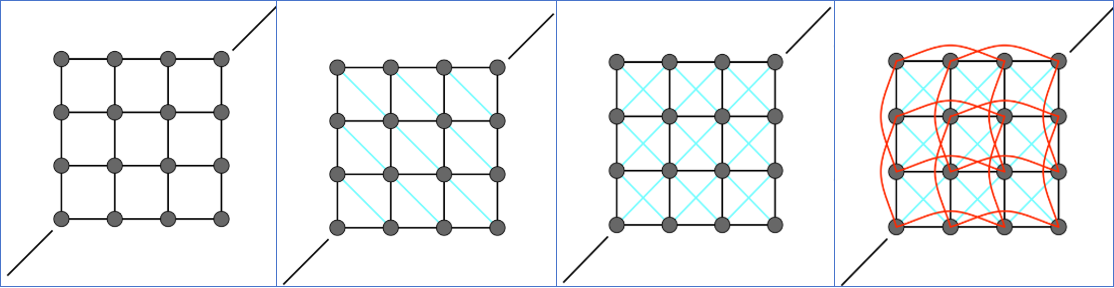
抗剪切(Shearing)
如果你只连横竖弹簧,这个网格在平面内稍微受力就会变成平行四边形,完全无法抵抗剪切力 。
对策:添加对角线弹簧 。这样网格就有了抵抗“斜向拉伸”的能力。
抗弯曲(Bending)
即使有了对角线弹簧,这块“布”还是可以沿着网格线轻易折叠,像纸一样产生死褶 。
对策:添加跨越一个质点的弯曲弹簧(Bend Springs) 。
为什么要这样做:它连接了质点 1 和质点 3(跳过质点 2),通过这种远程约束,限制了布料在平面外的弯曲幅度,从而模拟出布料的柔韧感 。

质点弹簧系统总结:
原子化:把复杂的物体拆解为有质量的点(Mass) 。约束化:用弹簧定义点与点之间的物理约束(Spring) 。迭代化:在每一帧计算所有弹簧产生的合力,更新位置 。
这种方法的优点是极其简单、直观且容易实现 。但它的缺点在于,当弹簧刚度 $k_s$ 非常大时,数值计算会变得极不稳定,这促使了后来更高级方法(如显式/隐式积分或有限元分析 FEM)的发展 。
粒子系统(Particle Systems)
Note 质点弹簧系统是为了模拟有“组织结构”的物体(如布料),那么**粒子系统(Particle Systems)**则是为了模拟那些“无固定形状”或“成群结队”的模糊现象 。
因为在模拟烟雾、火焰、爆炸或者成群的飞鸟时,使用复杂的几何网格既不符合物理直觉,也会让计算量爆炸 。

粒子系统的核心逻辑非常简单:将复杂的动力学系统简化为大量微小质点的集合 。
极简的个体:每个粒子通常只携带位置、速度、质量和生命周期(Life)等基本属性 。计算的解耦:在最简单的情况下,粒子之间互不影响。这意味着你可以轻松地通过增加粒子数量来提升视觉复杂度(Scalability),而不需要重写核心算法 。物理的普适性:无论是模拟银河系的引力,还是模拟水滴的喷溅,底层逻辑依然是那套牛顿定律 $F=ma$ 。
粒子的“一生”是如何度过的?
为了在屏幕上看到动态的效果,计算机在每一帧都要为每个粒子执行一个完整的“生命循环” :
新生(Generate):在发射器(Emitter)位置根据概率或特定规则生成新粒子 。受力(Calculate Forces):计算这一时刻粒子受到的所有外力 。演化(Update):根据受力更新速度和位置 。消亡(Remove):如果粒子撞击了边界,或者生命周期结束(例如烟雾飘散),就将其从内存中剔除 。绘制(Render):将粒子渲染为像素、小图块或模糊的光点 。
如何让粒子“动得自然”?
粒子系统之所以强大,是因为可以通过叠加不同的“力”来调制出完全不同的物理质感 :
引力与斥力(Attraction & Repulsion):
- 万有引力:模拟星系演化。公式遵从:$F_g = G \frac{m_1 m_2}{d^2}$
- 推进力:模拟火箭喷气或爆炸喷射 。
阻尼力(Damping Forces):如果没有空气阻力、摩擦力或粘滞力,物理模拟看起来会像在太空中一样永远停不下来 。碰撞(Collisions):让粒子能够与场景中的墙壁、地板甚至是角色的身体产生交互,这是实现沉浸感的关键 。
群体涌现(Flocking/Boids)
粒子系统最迷人的地方:简单的个体规则,如何演化出复杂的群体智能?
如果你想模拟一群鸟(Boids)或一群鱼,你不需要为每一只鸟编写复杂的路径规划。你只需要给每只“鸟粒子”设定三个极简的力学逻辑 :
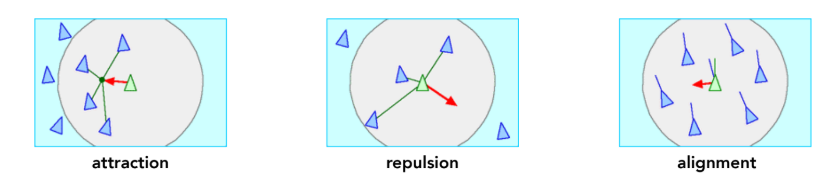
凝聚力(Cohesion):向邻居的中心靠拢。为什么要这样做?因为鸟群倾向于聚在一起增加安全感 。排斥力(Separation):避免与邻居靠得太近。为什么要这样做?为了避免在飞行中发生碰撞 。对齐力(Alignment):趋向于邻居的平均运动方向和速度。为什么要这样做?为了保持队形的连贯性 。
当成千上万个粒子同时遵循这三条规则时,就会惊讶地发现,屏幕上出现了极其真实的集群飞舞效果 。
Note 虽然粒子系统易于理解,但当要模拟极其细腻的流体(Fluid)时,可能需要数百万个粒子 。此时面临两个挑战:
计算压力:每个粒子都要计算邻居对它的影响。空间搜索:为了优化计算,我们需要加速度结构(Acceleration Structures),就像我们在光线追踪中学到的 BVH 或网格剖分一样,用来快速找到每个粒子附近的邻居 。
运动学
在模拟布料时,我们关心的是物理真实;但在模拟角色时,我们关心的是操控感和表演。

Tip 刚好最近阿凡达3上映,去看了一下,其离线渲染和合成能力确实是真假难分,图形学的顶级应用。
正向运动学 (Forward Kinematics, FK) —— 顺流而下

想象你在控制一个提线木偶。如果你转动木偶的肩膀,你会发现它的手肘和手指也会跟着移动。这就是正向运动学。
为什么要这样做:在计算机中,角色通常被建模为一个由关节连接的树状结构(Tree structure) 。当你改变父节点的旋转角度时,子节点的位置会随着坐标系的变换自动更新。
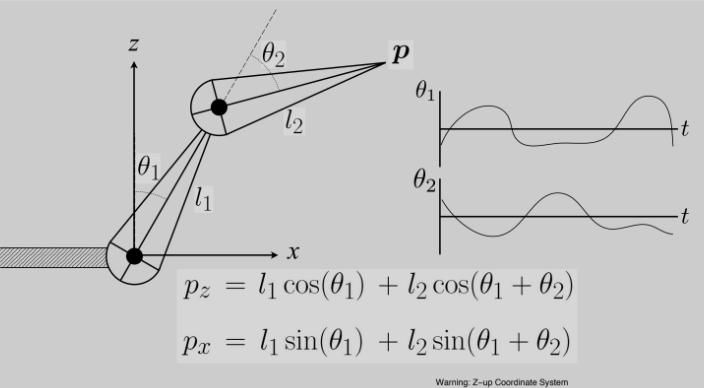
数学逻辑:在 2D 空间里,如果我们知道每一节骨骼的角度 $\theta$ 和长度 $l$,末端执行器(End Effector)的位置就是一系列三角函数的叠加 :
$$ p_x = l_1 \sin(\theta_1) + l_2 \sin(\theta_1 + \theta_2) $$$$ p_z = l_1 \cos(\theta_1) + l_2 \cos(\theta_1 + \theta_2) $$FK 的控制非常直接,实现起来也很简单 。它的痛点:如果你想让角色的手精准地握住桌上的杯子,用 FK 就非常痛苦。你需要反复调整肩膀、肘部、手腕的三个角度,直到手掌刚好碰到杯子 。
逆向运动学 (Inverse Kinematics, IK) —— 溯流而上
为了解决 FK 的痛苦,逆向运动学诞生了。
设计动机:动画师只想说“把手放在杯子上”,剩下的关节角度该如何摆放,交给计算机去算 。
为什么这是个难题?
- 多解性(Multiple solutions):手掌固定在空中,你的胳膊肘可以朝上,也可以朝下 。
- 无解性:如果你想让手伸向两米外,但胳膊只有一米长,方程就无解了 。
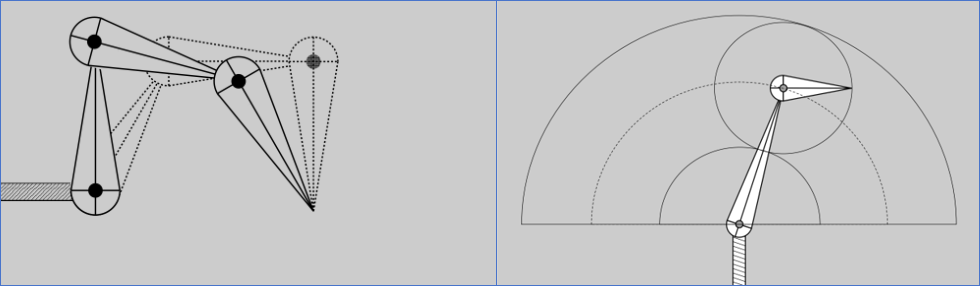
如上图所示,如果确定最后针尖的位置,那么可以存在无数个中间关节的位置和旋转角度;如果我们确定两个关节点的位置,那么最后一个针尖的位置可以存在于扇形面的任何位置中。
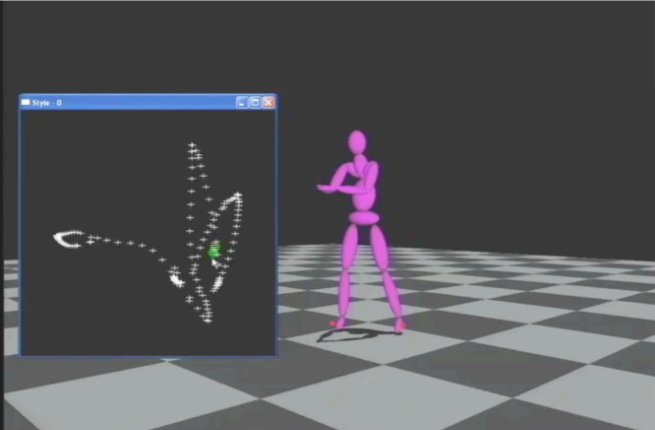
工程解法:由于对于多节骨骼,直接解三角方程极其困难,通常定义一个误差指标(Error metric)(例如当前手掌与目标的距离),然后使用**梯度下降(Gradient descent)**等优化算法,一步步把骨骼“拉”向目标位置 。
绑定 (Rigging) 与 混合形状 (Blend Shapes) —— 赋予灵魂
有了骨架,我们还需要让模型表面产生自然的形变。

绑定(Rigging):
为什么需要它:骨架只是点和线,绑定则是为角色创建一套高级控制句柄(类似于木偶的拉线)。绑定非常昂贵且费时,需要技术美术师手动设置模型顶点如何随骨骼运动产生拉伸和褶皱 。
混合形状(Blend Shapes):
为什么不只用骨骼? 人的面部表情极其微妙,单纯靠骨骼旋转很难模拟出皮肤的滑动。
核心逻辑:预先建模出几组典型的表情(如大笑、愤怒),然后在这些表情的顶点位置之间进行插值(Interpolate) 。
动作捕捉 (Motion Capture) —— 真实的数据驱动
当我们需要极高的真实感时,与其手动打关键帧,不如直接搬运现实世界的数据 。

为什么要这样做:人类的动作包含无数细微的扰动,这是手绘很难完全还原的 。

恐怖谷效应(Uncanny Valley):这是一个关键概念。当角色的外观和动作非常接近真实人类,但又存在一点点不自然时,人类会产生强烈的不适感和厌恶感 。这逼迫我们要么做夸张的卡通风格,要么就得追求极致的真实。
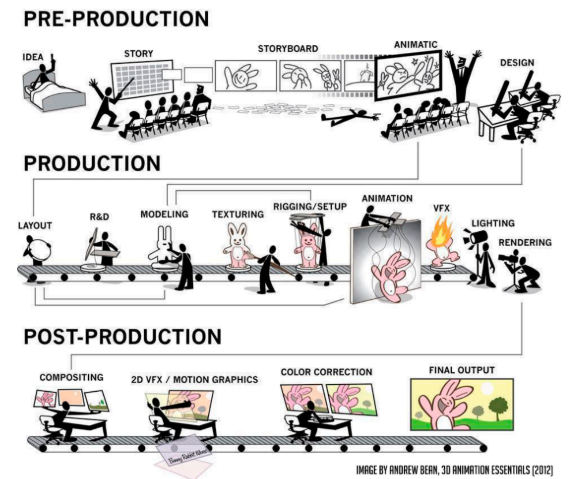
最后,动画是一个复杂的工业流程。课程总结了从一个**点子(Idea)到最终输出(Final Output)**的完整生命周期 :
前期制作:写故事、画分镜(Storyboard)、制作动态分镜(Animatic)。中期制作:建模(Modeling)、绑定(Rigging)、动画(Animation)、特效(VFX)、灯光与渲染 。后期制作:合成(Compositing)、调色(Color Correction)。
数值计算与动画模拟
Tip 这部分听课的时候走神了,没有特别理解透彻,后续看看找机会找补理解一下单粒子模拟。
动画模拟的核心任务是求解物体随时间的位置变化。在最简单的情况下,我们关注一个粒子的运动。
粒子的运动被定义为一个一阶常微分方程(ODE):$\dot{x} = v(x, t)$。
速度场:把空间想象成一个巨大的流场(类似小学三年级学过的磁场电场),粒子在每一个位置 $x$ 和时刻 $t$ 都有一个对应的速度 $v$。
数值积分:显式、隐式与稳定性
为了计算下一时刻的位置 $x(t + \Delta t)$,我们需要对速度进行积分。
显式欧拉法 (Explicit Euler)
显式欧拉法的做法是:用当前时刻的速度来预测下一时刻的位置。
$$ x_{n+1} = x_n + \Delta t \cdot v_n $$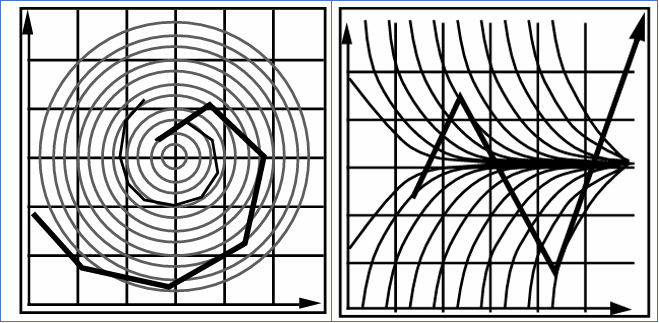
现实世界是连续的,而计算机是离散的。当你用一条切线(当前速度)去模拟一条曲线轨迹时,你永远在“过冲(Overshoot)”。能量不守恒:在圆周运动模拟中,显式欧拉会让质点每一帧都比圆周向外偏一点。结果就是质点轨迹变成了一个向外扩散的螺旋线,系统能量不断增加,最终“爆炸” 。
隐式欧拉法 (Implicit Euler)
为了解决爆炸问题,科学家提出了一个“反直觉”的想法:如果我们用未来时刻($t+1$)的速度来计算位置呢?
隐式欧拉法的做法是:用下一时刻的速度(未知量)来计算位置。
$$ x_{n+1} = x_n + \Delta t \cdot v_{n+1} $$它具有无条件稳定性(Unconditionally Stable),即无论你选多大的时间步长 $\Delta t$,它都不会爆炸。它倾向于丢失能量(数值阻尼)。在模拟中,系统变慢总比系统炸掉要好 。
代价则是:公式中等号两边都有未知数 $n+1$。这意味着你不能直接计算,而是要解一个复杂的方程组(通常需要牛顿迭代法),计算量显著增加。
中点法
显式欧拉看起点,隐式欧拉看终点。中点法则试图寻找一个平衡:先看一眼中点。
用显式欧拉走半步,到达中点 $a$,计算中点 $a$ 处的速度。回到起点,用中点的速度走完完整的 $\Delta t$。
从泰勒展开的角度看,中点法抵消了二阶误差项(Second-order accurate)。它比显式欧拉精确得多,且计算量增加很小。它像是在跳跃前先往前探了半个身子,看清路后再跳。
龙格-库塔法 (RK4):数值计算的“金标准”
追求极高的精确度(例如模拟精细的烟雾或复杂的布料),你会用到 RK4。
逻辑:它不仅看中点,它在区间内采样四个点的斜率(起点、两个中点预测、终点预测),然后取加权平均。
为什么要这样做?
因为它具有四阶精度,意味着误差是以 $(\Delta t)^4$ 的速度缩小的。它是目前科学计算和物理引擎中最广泛使用的显式积分算法,兼顾了稳定性和高精度。
流体模拟
在真实的物理模拟情况中,我们不再仅仅关心一个点,而是关心点与点之间的相互作用,以及物体如何维持其空间体积。
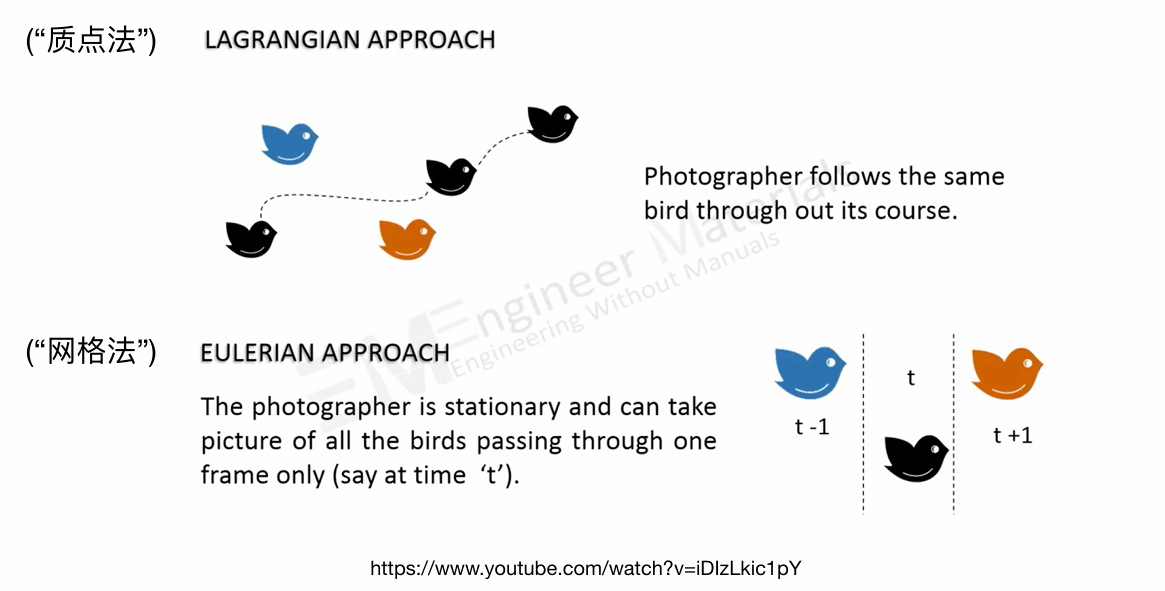
拉格朗日法 (Lagrangian Approach)
其核心逻辑:“跟着粒子走”。将流体看作无数个携带属性(质量、速度)的粒子。
代表算法:SPH (Smoothed Particle Hydrodynamics)。
为什么要这样做:在处理飞溅的水花、破碎的波浪时,粒子非常直观。
挑战:为了维持流体的体积不可压缩性,每个粒子需要感知周围邻居的压力。这需要定义一个“影响半径”(Kernel Function),计算非常耗时。
SPH(平滑粒子动力学)
粒子之间并没有连线,它们怎么知道自己是“一坨”水?
粒子是孤立的点,无法直接求导。SPH 引入了核函数 (Kernel Function)。每一个粒子都有一个“影响范围”。通过对半径 $h$ 内的邻居粒子进行加权平均,我们可以估算出任何位置的密度和压力梯度。
该方法的受力逻辑:密度约束:如果粒子挤在一起,密度变大,就会产生向外的排斥力。粘滞力:模拟液体内部的摩擦,让流动变得粘稠。
欧拉视角 (Eulerian Approach)
流体本身流动,但你的视点不动。空间被划分为固定的网格 (Grids),你只观察每个网格里流速、压力的变化。
这样做有两个好处:数学优雅:流体在宏观上是连续的场。在网格上求解偏微分方程(如压力场)比在乱动的粒子间计算要稳定得多。体积守恒:很容易强制要求进入格子的水等于流出格子的水,从而保证流体不“缩水”。
欧拉法虽然在处理压力和表面平滑度上非常优秀,但它很难表现极其细微的飞溅,且存在“数值耗散”(水流动着动着就消失了)。
为什么要引入混合方法 (Hybrid Methods)? 为了结合两者的优点,现代电影特效(如《阿凡达》、《冰雪奇缘》)最常使用的是 FLIP (Fluid-Implicit Particle) 算法:
粒子存储信息:位置和速度存在粒子上(拉格朗日),保证细节不丢失。网格计算受力:将粒子速度映射到网格,在网格上求解压力方程(欧拉),保证体积不压缩。反馈更新:把算好的新速度传回粒子。
刚体与碰撞
流体模拟不仅仅是水本身,还涉及它与环境的交互。
为什么要使用冲量 (Impulse) 而不是力? 在处理流体撞击杯壁时,碰撞发生的时间极短。模拟复杂的受力过程非常不稳定,因此我们直接修改粒子的速度向量,确保它不会穿透固体表面 。
刚体模拟 (Rigid Body): 与质点不同,刚体具有惯性张量 (Inertia Tensor)。当流体冲击刚体边缘时,不仅会产生平移,还会产生力矩 (Torque) 导致物体旋转。
Important 离散与连续的平衡:粒子负责“形”,网格负责“质”。
稳定性高于一切:在实时渲染或复杂动画中,一个绝对稳定(不会爆炸)的隐式求解器往往比追求绝对物理真实的算法更重要。