几何是计算机图形学中三维建模与渲染的基础,应用于物体建模、几何变换和碰撞检测等领域。其表示方法主要分为隐式表示(如代数曲面、水平集和距离函数)和显式表示,用于描述不同复杂度的形状。
几何概念
Tip 个人感觉本章前面的内容有点空洞和理论,建议直接快速浏览,从几何处理部分看起。
几何的应用(Applications of Geometry)
在图形学中,几何不仅仅关乎抽象的数学对象,它是三维建模和渲染的基础。以下是几何学的几个应用领域:
物体建模:通过几何学,计算机可以表示任何形状,例如从简单的几何体(如球体、立方体等)到复杂的自由形状(如汽车、人物模型等)。
几何变换:在渲染和动画中,物体的形状需要根据不同的需要进行变换,例如平移、旋转、缩放等。这些变换都可以通过几何学的运算来实现。
碰撞检测:几何学还用于物理引擎中的碰撞检测,确保虚拟世界中的物体不会穿透或重叠。

几何表示(Representations of Geometry)
隐式表示(Implicit Representations)
隐式表示并不是直接通过列举点或多边形来描述物体的表面,而是通过某个数学方程或函数来定义物体的几何形状。隐式表示方法通过一个方程或函数来表示物体表面上的所有点。这些函数通常被用来定义物体的边界或表面。
代数曲面(Algebraic Surfaces)

代数曲面是通过代数方程来描述物体的形状。最简单的例子是球体,它可以通过方程 $x^2 + y^2 + z^2 = r^2$ 来表示。这种表示方法非常直观,适合表示对称性较好的几何形状,但对于复杂图形无能为力。
水平集(Level Sets)
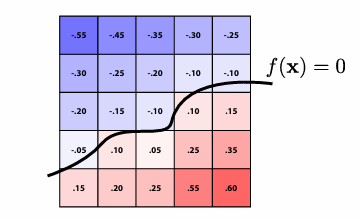
水平集是一种使用数学函数来表示几何物体的方式。具体来说,水平集方法使用一个标量场(scalar field) $f(x, y, z)$ 来表示物体的形状。物体的表面是通过找到函数值为0的点来确定的。例如,球体可以表示为函数 $f(x, y, z) = x^2 + y^2 + z^2 - r^2$ 的零水平面。
水平集方法常用于模拟流体、气体、柔体物体等,其优点是能够自然地表示拓扑变化(如合并或分裂),非常适合动态模拟。
距离函数(Distance Functions)
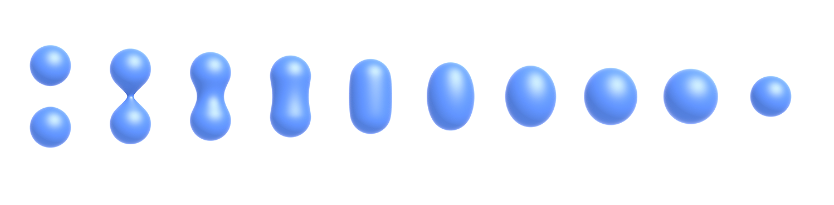
距离函数表示物体表面的每一点到物体表面最近点的距离。对于球体,距离函数是 $d(x, y, z) = \sqrt{x^2 + y^2 + z^2} - r$,其中 $r$ 是球体的半径。
距离函数配合插值可以通过简单的数学操作实现物体的融合等变换。
显式几何表示(Explicit Representations)
显式表示方法是通过直接列出物体的几何表面上的点、边或面来表示物体。显式表示通常使用网格或曲面来表示物体的表面,适用于大多数静态几何形状和计算机图形学中的渲染。常见的显性表示方法有:
点云(Point Cloud)

点云表示物体的表面通过一组离散的点来表示。每个点有自己的三维坐标,所有这些点共同描述了物体的形状。点云通常用于通过3D扫描(如激光扫描)获取的实际物体模型,或者在某些特定的计算机视觉应用中(如表面重建)。
多边形网格(Polygon Mesh)

多边形网格是最常见的几何表示方法,它通过一组连接在一起的多边形(通常是三角形或四边形)来表示物体的表面。每个多边形由顶点、边和面组成。多边形网格可以非常灵活地表示复杂的几何形状,广泛应用于3D建模、动画和游戏中。多边形网格的顶点通常通过顶点坐标、法线、纹理坐标等属性来描述。
细分曲面(Subdivision Surfaces)

细分曲面是一种基于细分方法生成平滑曲面的技术。它从一个较为粗糙的多边形网格开始,通过递归细分每个面(例如四边形或三角形)来生成更加光滑的曲面。细分曲面技术被广泛用于需要光滑曲面建模的领域,例如汽车外形、人物建模等。典型的细分曲面算法有Catmull-Clark细分和Doo-Sabin细分。
NURBS(非均匀有理B样条,Non-Uniform Rational B-Splines)
NURBS是一种基于样条曲线和曲面的表示方法,它允许非常精确地描述曲线和曲面。通过NURBS,可以表示出既平滑又准确的复杂几何形状。NURBS广泛应用于工业设计、建筑设计等领域,尤其适合表示复杂的自由曲面。
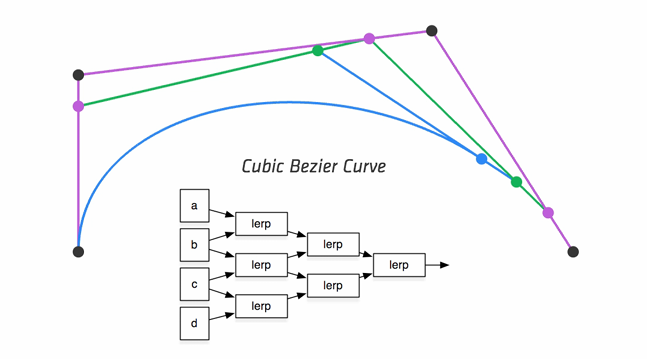
Bezier 曲线(Bézier Curves)
在计算机图形学中,Bezier 曲线是非常重要的工具,广泛应用于字体设计、动画插值、路径绘制等领域
三次 Bézier 曲线由 4 个控制点定义,分别为:
- $p_0$ 起点
- $p_1$ 起点处的控制点,决定曲线的初始切线方向
- $p_2$ 终点处的控制点,决定曲线的结束切线方向
- $p_3$ 终点
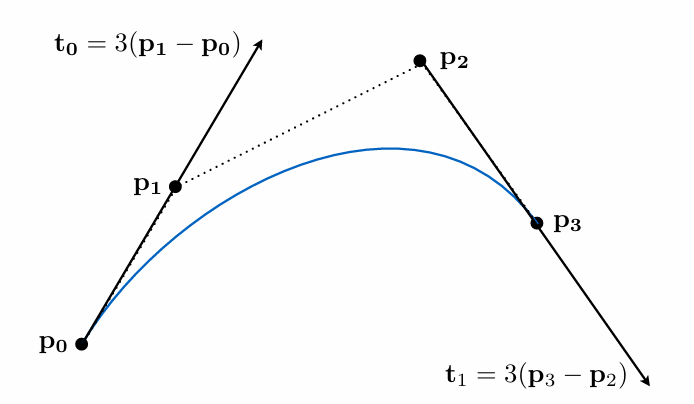
这四个点共同决定了曲线的形状。Bezier 曲线的一个显著特性是,曲线始终在由这些控制点构成的凸包内部,这保证了曲线的形状可控。
de Casteljau 算法:计算 Bézier 曲线
de Casteljau 算法是一种递归方法,用于计算任意阶数的 Bézier 曲线。该算法使用 线性插值(lerp)不断地缩小控制点的范围,直到找到曲线的精确位置。对于二次 Bézier 曲线(3 个点)而言,计算过程如下:
- 首先在 $b_0$ 和 $b_1$ 之间做线性插值,得到点 $b^0_1$
- 接着在 $b_1$ 和 $b_2$ 之间做线性插值,得到点 $b^1_1$
- 最后对这两个点 $b^0_1$ 和 $b^1_1$ 做线性插值,得到最终的曲线点 $b^0_2$
对于三次 Bézier 曲线(4 个点),则递归地将每两个控制点进行插值,最终通过四层递归计算得到曲线上的点。
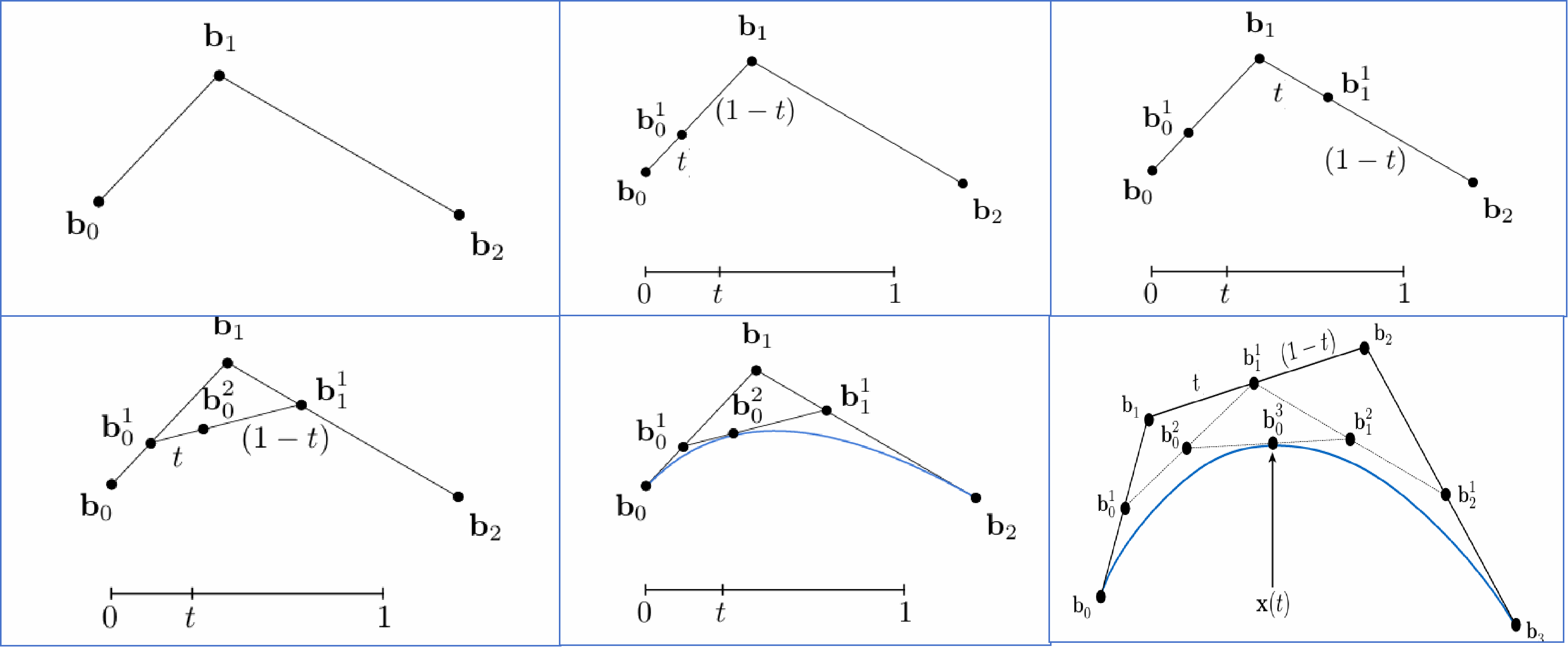
这一方法直观且稳定,适用于计算机图形学中对曲线的实时渲染。
Bézier 曲线的代数表达式
除了使用 de Casteljau 算法外,Bézier 曲线还可以通过 代数公式进行表示。对于三次 Bézier 曲线,其代数形式为:
$$ b(t) = (1-t)^3 b_0 + 3t(1-t)^2 b_1 + 3t^2(1-t) b_2 + t^3 b_3 $$该公式中的每一项使用了 Bernstein 多项式,其中 $B_i^3(t)$ 是基函数。Bernstein 多项式的性质使得 Bézier 曲线在 $t = 0$ 和 $t = 1$ 处分别插值起点和终点,并且控制点的数目决定了曲线的阶数。
Bézier 曲线的重要性质
Bézier 曲线有几个重要的几何性质,这些特性使得它在图形学中非常有用:
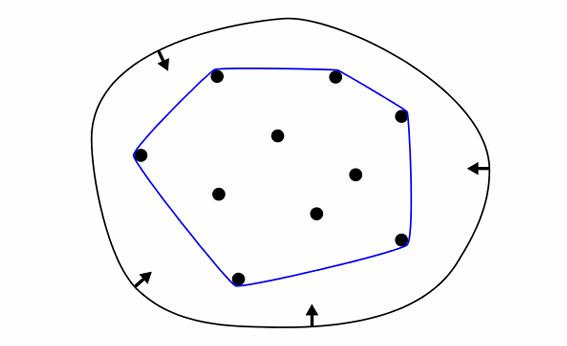
- 插值端点:曲线一定通过起点和终点,保证了其起始和结束位置的精确性。
- 端点处切线方向:三次 Bézier 曲线的切线方向由起点到第一个控制点的向量决定,从而提供了端点处的方向性。
- 仿射不变性:对控制点进行平移、旋转或缩放变换时,曲线形状保持不变,只会随控制点的变换而变。
- 凸包性质:曲线始终位于其控制点构成的凸包内,这一点保证了曲线不会脱离设计范围。
这些特性使得 Bézier 曲线非常适合用于路径设计和动画控制。
分段 Bézier 曲线(Piecewise Bézier Curves)

由于高阶 Bézier 曲线(控制点超过 4 个)难以控制和调整,实际应用中通常采用 分段 Bézier 曲线。将多条低阶 Bézier 曲线拼接起来,可以实现复杂的曲线形状,同时保持每段曲线的平滑性和可控性。
例如,在字体设计中,字形曲线通常是通过多个三次 Bézier 曲线连接形成的。为了保证连接处的平滑性,分段 Bézier 曲线通常要求满足 C⁰ 连续性(位置连续)和 C¹ 连续性(切线连续),即连接处的曲线要在位置和切线方向上无缝衔接。
分段 Bézier 曲线的广泛应用使其成为图形设计中非常重要的工具。
双三次 Bézier 曲面片段
Bicubic Bézier Surface Patch双三次 Bézier 曲面片段是 Bézier 曲线扩展到曲面上的应用,它是 3D 图形学中用于表示平滑曲面的一种方法。这个部分是计算机图形学中的高级内容,通常用于描述复杂的曲面。
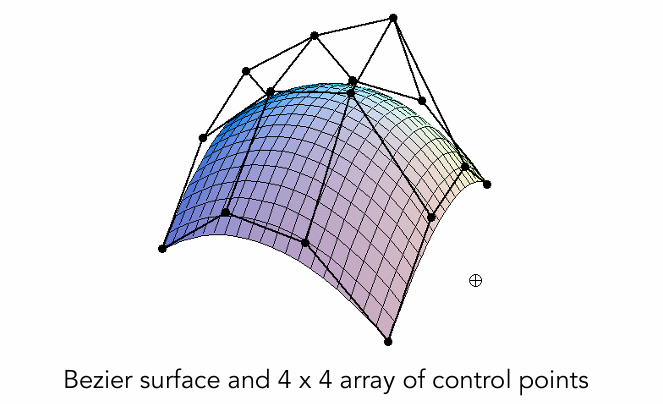
Bicubic Bézier 曲面是通过 4×4 个控制点来定义的,类似于一条三次 Bézier 曲线通过 4 个控制点来定义,但这里是二维的曲面,而非一维曲线。每个控制点是一个 3D 点,具有 x, y, z 坐标。通过这些控制点,可以描述一个曲面。
这个曲面的参数化是通过两个变量 $u$ 和 $v$ 来进行的,分别表示曲面上点的位置:
- $u$ 表示在 横向方向(从左到右)上的变化
- $v$ 表示在 纵向方向(从上到下)上的变化
这两个参数都在区间 [0, 1] 之间变化。
Bicubic Bézier 曲面定义需要 16 个控制点,这些控制点组织成一个 4×4 的控制点网格。在这个网格中,每个点 $P_{ij}$ 的位置是一个三维坐标点 $P_{ij} = (x_{ij}, y_{ij}, z_{ij})$,其中 $i$ 和 $j$ 分别表示横向和纵向的索引。
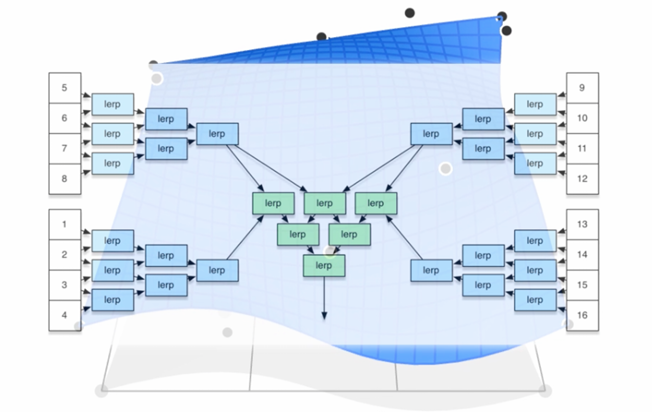
计算 Bicubic Bézier 曲面上的点
为了计算曲面上某个位置的点,我们需要确定两个参数 $u$ 和 $v$ 对应的曲面位置。这个计算通过在两个方向上分别应用 de Casteljau 算法 来完成,最终得到一个表面上的点。
步骤一:沿着 $u$ 方向插值
首先,沿着 $u$ 方向对每一行的 4 个控制点进行线性插值(de Casteljau 算法),得到 4 个新的曲线,这些曲线表示了在 $v$ 固定时,沿 $u$ 方向的变化。
假设 $u$ 为给定的参数值,那么对于每一行控制点 $P_{i0}, P_{i1}, P_{i2}, P_{i3}$,我们可以按照 de Casteljau 算法计算出新的插值控制点 $Q_i(t)$,即:
$$ Q_0 = (1 - u)P_{00} + uP_{01} $$步骤二:沿着 $v$ 方向插值
然后,沿着 $v$ 方向对刚才得到的 4 个插值点 $Q_0, Q_1, Q_2, Q_3$ 进行再次插值,得到最终曲面上的点 $P(u, v)$:
$$ P(u, v) = (1 - v)Q_0 + vQ_1 $$通过这个过程,我们可以计算出任意 $u$ 和 $v$ 对应的曲面上的点。最终,$P(u, v)$ 就是位于给定参数值 $u$ 和 $v$ 的曲面上的点。
几何处理Geometry Processing
Mesh Operations: Geometry Processing(网格操作:几何处理)是计算机图形学中的一个重要概念,涉及对3D模型网格的各种操作。网格是由顶点、边和面构成的结构,在图形学中,网格用于表示3D物体的表面。几何处理则指的是一系列操作,用于改变或优化网格的形状、质量或性能,以满足不同应用的需求。
网格细分(Mesh Subdivision)
网格细分是将粗糙的网格进行更精细的分割,目的是使得网格表面更加平滑。这个过程通常通过将每个面进一步细分为更多的小面来完成。细分操作的典型例子有 Catmull-Clark细分 和 Loop细分,它们都能产生更光滑、更高细节的网格。

Loop Subdivision
Loop 细分是一种用于 三角网格 的细分算法,它的基本思想是将每个三角形面分割成四个更小的三角形,并调整顶点的位置,使得网格表面更加平滑。
Tip Loop Subdivision方法的Loop和循环没有关系,是因为科学家的家人姓Loop。(●’◡’●)
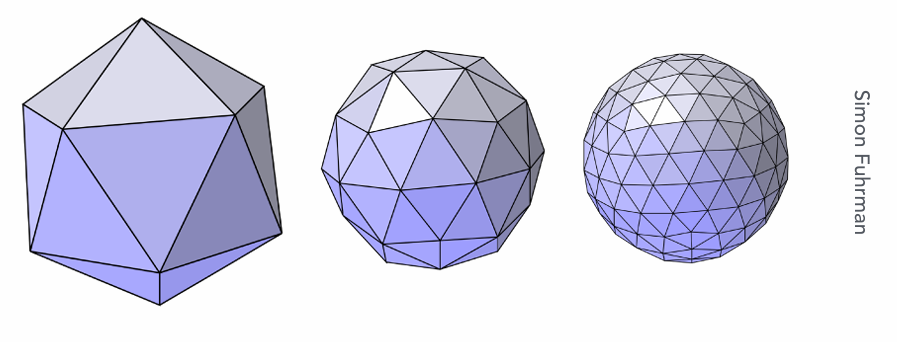
Loop 细分步骤
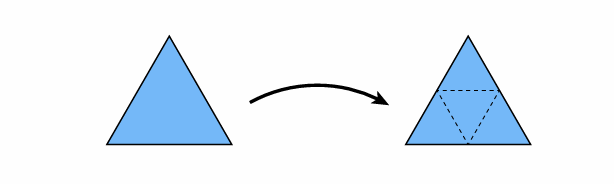
- 步骤 1:细分三角形 每一个三角形都会被分割成四个更小的三角形。在原网格的每一个三角形中,算法会插入一个新的顶点,将每个三角形分割成四个小三角形。这些新顶点的位置是通过对原有三角形的顶点进行加权计算得到的。
- 步骤 2:更新顶点位置 更新新顶点的位置时,原始顶点和新顶点的位置是通过不同的加权系数来计算的。新顶点的更新通常基于周围邻域的顶点的加权平均位置。
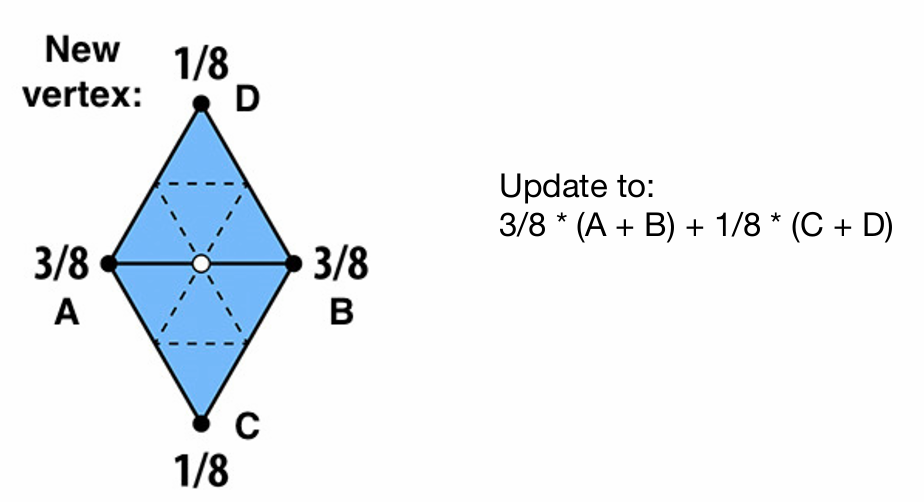
例如,对于三角形的一个新顶点的计算,Loop 细分使用以下方式:
$$ \text{新顶点位置} = \frac{3}{8} \times (A + B) + \frac{1}{8} \times (C + D) $$其中 $A, B, C, D$ 是原始三角形的顶点。
- 步骤 3:处理旧顶点 对于原来的顶点(即,三角形的顶点),它们也会被更新。更新方法考虑了该顶点与相邻顶点的关系,通常使用以下公式:
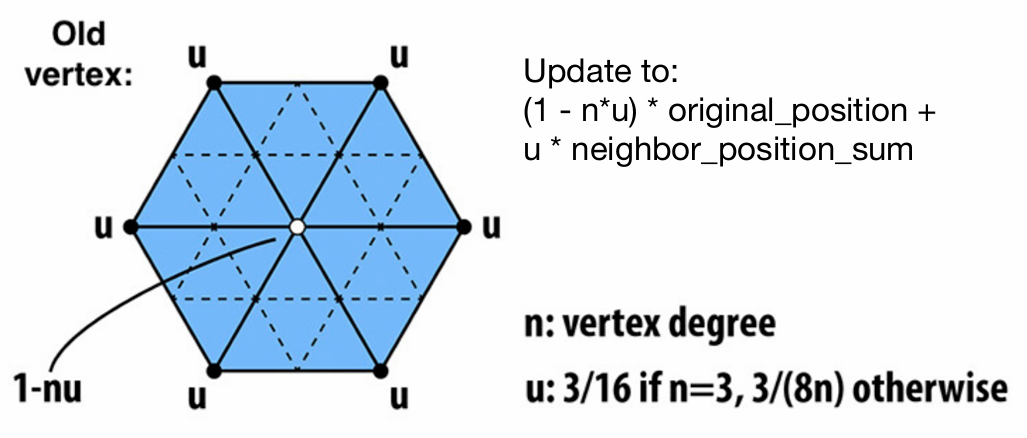
其中,$n$ 是顶点的度数(邻居数量),$u$ 是一个权重因子,决定了更新位置的偏移程度。
通过不断重复这些步骤,网格逐渐变得更加光滑和精细。Loop 细分常用于 三角网格,特别是需要高分辨率且平滑表面的场景。
Catmull-Clark Subdivision
Catmull-Clark 细分是一种 面向四边形网格的细分算法,但它同样可以处理 非四边形网格。当一个网格中的某些顶点的度数不为四(即顶点的连接边数不等于四时),这些顶点被称为 奇异点(Extraordinary vertices)。
奇异点的定义
在 Catmull-Clark 细分中,奇异点指的是 度数不等于四的顶点。例如,一个顶点可能与三条边相连(度数为3),或者与五条边相连(度数为5),这些顶点就被视为奇异点。
- 对于常规的 非奇异顶点(度数为4的顶点),细分时会按照标准的更新规则进行更新。
- 而对于 奇异点,细分时需要采取特殊的处理方法。
奇异点的处理
在 Catmull-Clark 细分过程中,奇异点的更新需要特别注意。由于奇异点的度数不为四,它的 位置更新规则 与普通顶点有所不同。为保证细分后的网格仍然平滑,并且能够处理多边形面,Catmull-Clark 细分算法在细分过程中会特别处理这些奇异点。
具体来说,奇异点的更新通常依赖于该点的 邻域结构(即连接该点的面和顶点的布局)。在更新过程中,算法会利用该点周围的邻域信息来计算它的新位置。
算法步骤
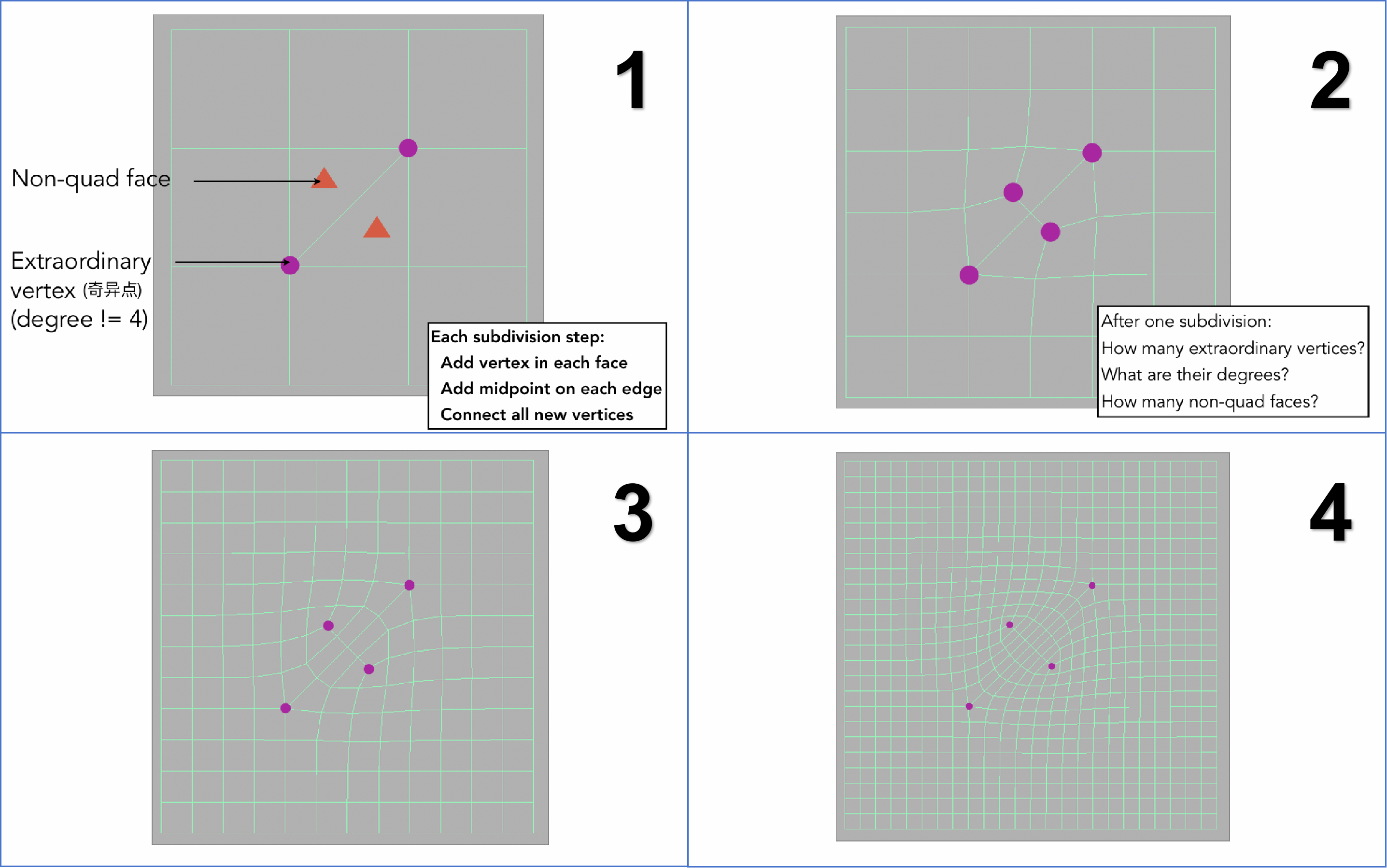
每个面(面片)添加新顶点: 在每个面(如四边形面或非四边形面)中,添加一个新的 面顶点。面顶点的位置是通过当前面上四个顶点的加权平均来计算的:
$$ \text{面顶点位置} = \frac{v_1 + v_2 + v_3 + v_4}{4} $$其中 $v_1, v_2, v_3, v_4$ 是面上的四个顶点。
每条边添加新顶点: 每条边的中点位置也是新的顶点。这个 边顶点 是通过计算当前边的两个端点和相邻面顶点的加权平均来得到的。公式如下:
$$ \text{边顶点位置} = \frac{v_1 + v_2 + f_1 + f_2}{4} $$其中 $v_1, v_2$ 是边的两个端点,$f_1, f_2$ 是与该边相邻的两个面的面顶点。
每个顶点更新位置: 对于原网格中的每个顶点,更新其位置。这些原始顶点的位置更新不仅仅取决于它们自己的位置,还依赖于它们周围邻域的顶点。更新公式如下:
$$ \text{更新顶点位置} = \frac{f_1 + f_2 + f_3 + f_4 + 2(m_1 + m_2 + m_3 + m_4) + 4p}{16} $$其中:
- $f_1, f_2, f_3, f_4$ 是与顶点相邻的四个面顶点。
- $m_1, m_2, m_3, m_4$ 是与该顶点相邻的四个边顶点。
- $p$ 是原顶点的原始位置。
通过这些步骤,Catmull-Clark 细分能够使网格更加平滑,同时保持原始几何形状的轮廓。
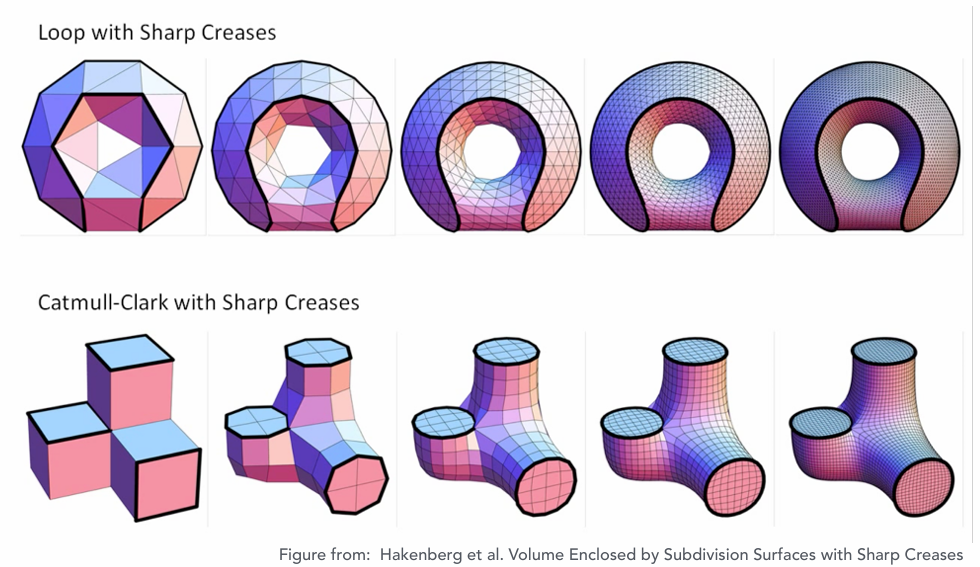
细分的收敛性与形状
细分算法的 收敛性 指的是经过多次细分后,网格最终趋向于某种平滑形状的能力。不同的细分算法在处理带有 锐角 或 硬边(creases) 的形状时表现不同。
- Loop 细分 在带有锐角或硬边的地方可能会导致不够精细的处理。
- Catmull-Clark 细分 对于带有硬边的形状能更好地保持这些特征,通常在处理复杂形状时效果更好。
网格简化(Mesh Simplification)
Mesh Simplification 的目标
网格简化的目标是 减少网格的分辨率,即减少顶点、边和面数,目的是:
- 提高渲染性能:降低网格的复杂性,使得渲染过程更加高效。
- 保持形状和外观:在简化过程中,尽量保持网格原有的形状和外观,使得简化后的模型与原模型相似。
具体来说,简化过程中会通过优化顶点和面片的数目来减少计算量,同时 避免过多失真,确保简化后的网格仍能准确地表示物体的主要特征。

Tip 如果网格简化效果不好,那就让美工回去重建嘻嘻(●’◡’●)
边坍缩(Edge Collapse)
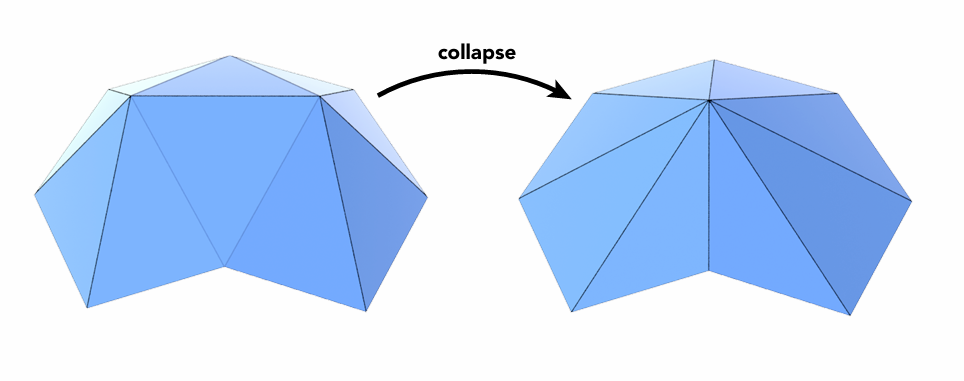
最常见的网格简化方法之一是 边坍缩,也叫做 边合并。该方法的基本思想是 合并相邻的边和顶点,通过这种方式,简化网格中的面片数量。
- 步骤:选择一条边,将该边的两个端点合并为一个新顶点,原来的面片被更新或删除,从而减少了网格的复杂度。
- 效果:每次合并一条边可以减少两个顶点和一条边,从而减少了面片数。通过重复这一操作,可以显著降低网格的面数和顶点数。
在进行边折叠时,通常需要计算 几何误差,以确保合并后的新顶点不会引起形状失真。
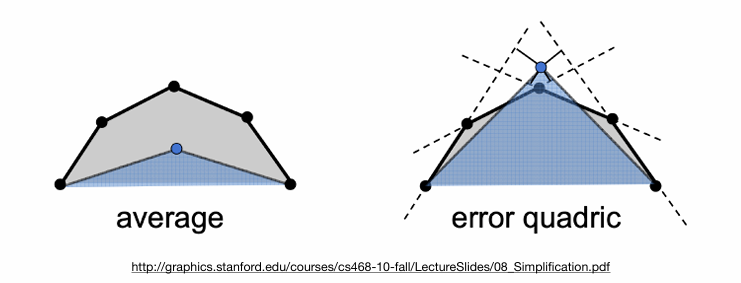
如何计算几何误差?
为了确保网格简化后保持良好的形状,通常会使用 几何误差度量。几何误差是指合并顶点时,简化后的顶点与原始位置之间的差异。常见的误差度量包括:
- 二次误差(Quadric Error Metric):一种常用的误差度量方法,它衡量的是合并顶点后与原始三角形面之间的距离。通过这种方法,可以评估每次顶点合并时引入的误差大小,从而选择合适的边进行合并。
- 原理:每次简化时,通过计算新顶点到原三角形的距离,尽量选择那些对几何形状影响最小的边进行折叠。
- 边折叠误差:在合并每一条边时,选择使误差最小化的顶点进行合并。
Tip 这里的基于二次误差去不断尝试去规划到底坍缩哪一条边,有点类似于深度学习中的以梯度下降损失函数收敛为目标的训练步骤
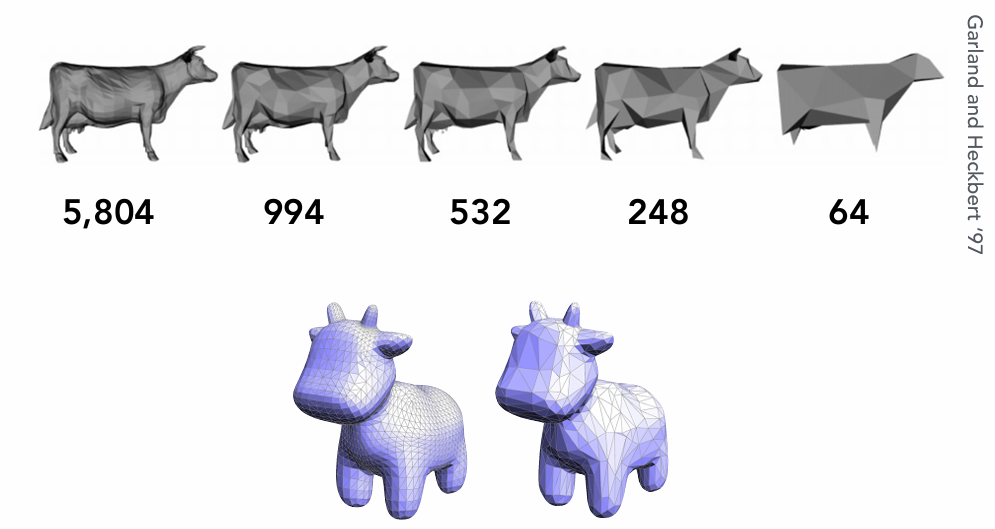
在网格简化后,网格的复杂性会显著降低,渲染速度提高,但简化的程度取决于具体应用的需求。例如,在某些游戏场景中,较低分辨率的网格可以大大提升渲染效率,尤其是在需要实时渲染的情况下。简化后的网格可以通过 不断迭代折叠边缘 来逐渐达到目标面数,同时最大限度地保留物体的形状细节。
如上图所示,边坍缩以后的牛牛还是尽量保持了原有的形态特征的。
网格正则化(Mesh Regularization)
网格正则化(Mesh Regularization) 是计算机图形学中用于改善网格质量的一个重要技术,特别是在网格优化和几何处理时。它的目标是 调整网格中顶点的分布,以达到 更均匀的网格分布,进而优化后续的处理过程,如渲染、模拟等。正则化的核心是通过改变顶点的布局或位置,使得网格的质量更加平衡,从而提高网格的稳定性和准确性。
为什么要正则化?
在原始的三维数据获取过程中,无论是通过 3D 扫描生成的点云重建,还是经过复杂的布尔运算,往往会产生大量极度扁平或细长的“退化三角形”。这些畸形单元在数值计算中会导致雅可比矩阵(Jacobian Matrix)条件数恶化,从而引发物理模拟(如布料动力学或流体计算)中的计算发散,或在渲染时产生糟糕的锯齿与伪影。
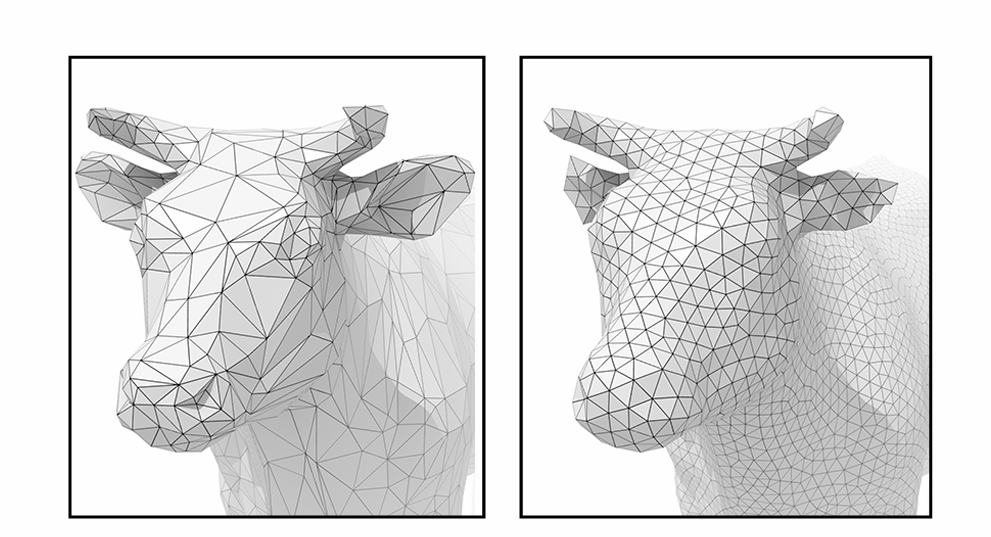
网格正则化通常有以下几种常见操作:
顶点重新定位(Vertex Relocation)
这一方法通过 移动顶点的位置,使得顶点分布更加均匀。通常,优化方法会基于网格的局部几何结构来决定每个顶点的新位置,使得网格面片的形状更加规整。
目标:使得每个面片(例如三角形或四边形)的大小、形状相对均匀,避免出现极长或极小的三角形/四边形。
方法:计算每个顶点的“拉力”或“压力”,然后调整顶点位置,通常是根据其邻域顶点的布局和网格局部的变化来决定。
拉普拉斯平滑(Laplacian Smoothing)
拉普拉斯平滑是一种常见的网格正则化技术,它通过计算每个顶点与其邻域顶点的 平均位置 来平滑网格。
原理:每个顶点的位置将被调整为该顶点邻接顶点的位置的加权平均。
步骤:将顶点位置与邻域顶点的平均位置进行对比,调整顶点位置,使得局部网格更加平滑。
效果:减少网格中突兀的角落或尖锐的区域,使网格更加均匀和平滑。
网格均匀化(Mesh Uniformization)
网格均匀化技术的目标是通过调整顶点的位置,使得网格的 顶点分布更加均匀,尤其是在曲面或复杂形状的情况下。这通常涉及将顶点重新分布,使得 每个面 的大小大致相同,避免某些区域的顶点过于稠密或稀疏。
方法:可以使用迭代优化算法,基于目标函数(如顶点分布的均匀性)进行优化。
目标:使得网格的各个部分在分辨率上保持一致,以避免出现 不规则的变形 或 局部失真。
局部平滑(Local Smoothing)
局部平滑是一种针对特定网格区域的正则化操作,它通过对网格的一部分(例如某个面片或某些顶点)进行平滑,改善局部几何结构。
方法:只对选定区域内的顶点进行平滑,而不影响整个网格。常用于处理网格中局部结构不平衡的情况。
效果:改善局部区域的质量,同时保持全局形状不变。