阴影贴图是光栅化渲染中生成阴影的主流技术。其核心思想是:一个点被照亮需同时被相机和光源可见。算法分为两步:首先从光源视角渲染生成记录最近距离的深度图;然后在相机视角渲染时,将每个点投影回光源视角,对比其实际距离与深度图记录值,以判断该点处于光照还是阴影中。
要讲述光线追踪,首先需要先引入之前的光栅化中的一个内容–阴影贴图
先导
阴影贴图 (Shadow Mapping)
为什么需要 Shadow Mapping?
在光栅化渲染中,我们通常是一个三角形一个三角形地画,很难直接知道“谁挡住了谁”从而产生阴影 。为了解决这个问题,我们引入了 Shadow Mapping。
- 定位:这是目前最主流的阴影生成技术,从早期的《玩具总动员》到《塞尔达传说:荒野之息》、《超级马里奥:奥德赛》等现代游戏都在使用 。
- 本质:它是一种图像空间 (Image-space) 的算法 。这意味着它依赖生成的图像(深度图)来计算,而不需要一直纠缠于复杂的场景几何数据。

Shadow Mapping 的核心思想非常朴素,只有一句话:
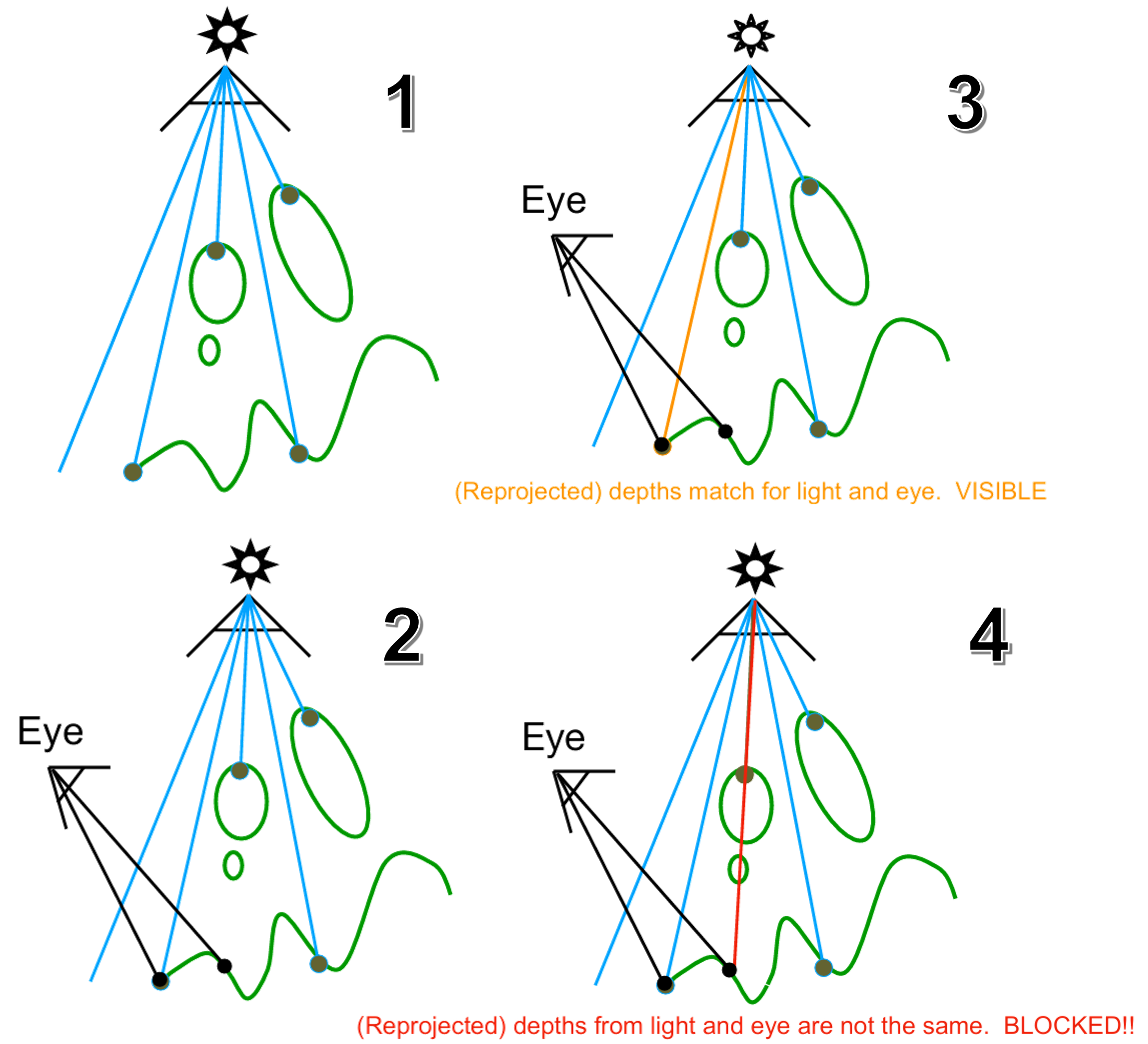
如果一个点不在阴影里,那么它必须能同时被“摄像机”和“光源”看到。
如果不被阴影覆盖(也就是被照亮),说明那个点既能被你的眼睛(相机)看见,也能被头顶的太阳(光源)直接照射到。如果那个点被太阳“看不见”(中间有障碍物挡住了),那它就在阴影里。
算法流程:经典的“两步走” (2-Pass)
Shadow Mapping 之所以叫 Mapping,就是因为它需要生成一张图(Map)。整个过程分为两次渲染:
第一步:光源视角的“彩排” (Pass 1: Render from Light)
- 做什么:把摄像机挪到光源的位置,看向场景,进行一次渲染 。
- 记什么:我们不关心颜色,只关心深度 (Depth)。生成的这张图叫 Shadow Map(阴影贴图/深度图)。
- 意义:这张图记录了从光源出发,在这个方向上能看到的最远的物体离光源有多近。换句话说,任何比这个距离更远的东西,都会被挡住。
第二步:相机视角的“实拍” (Pass 2: Render from Eye)
- 做什么:把摄像机放回正常的观察位置,开始渲染画面 。
- 怎么算:对于画面上的每一个可见点(Pixel),我们做一个“灵魂拷问”——“光源能看见你吗?”
- 操作:把这个点投影回光源的视角 。
- 对比 (Compare):
- 测量 “当前点到光源的实际距离”。
- 查看 Shadow Map 上对应位置记录的 “光源能看到的最近距离”。
判定结果 (The Verdict):

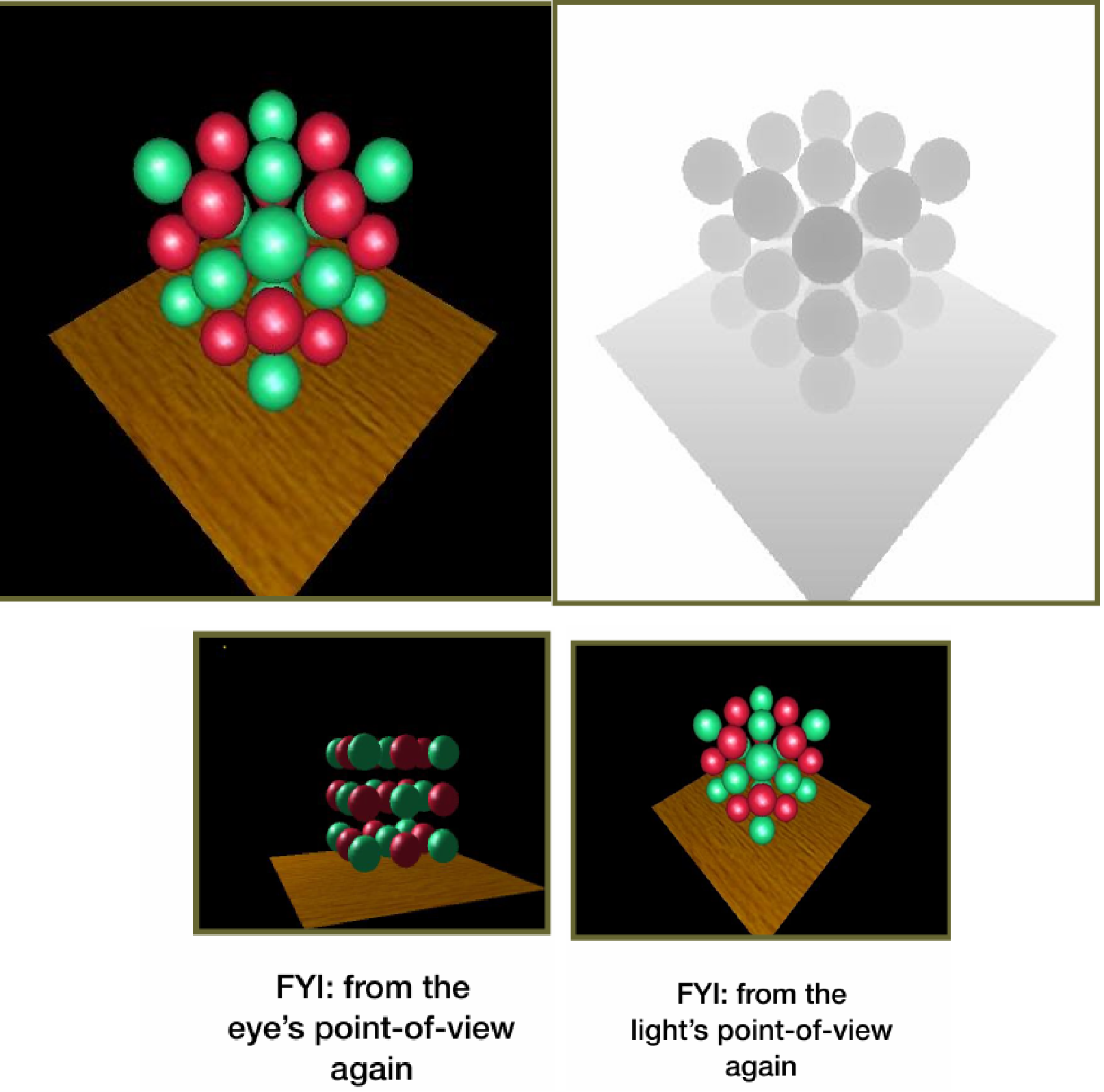
- ✅ 被照亮 (Lit):如果 实际距离 $\approx$ 记录的最近距离。说明中间没有障碍物,光源直接照到了它(上图中显示为绿色区域)。
- 🚫 在阴影中 (Shadow):如果 实际距离 $>$ 记录的最近距离。说明光源在更近的地方遇到了障碍物,当前点躲在了障碍物后面(上图中非绿色区域)。
Note 可以总结为一句口诀:先从光源看一遍(记深度),再从相机看一遍(比深度)。
Shadow Mapping 的“痛点”与局限
虽然这个算法很强,但它并不完美。主要有以下三个问题 :
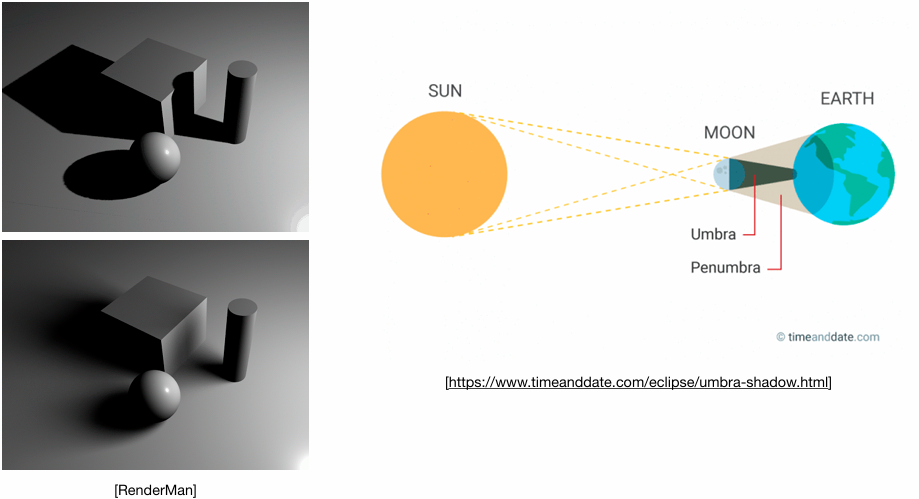
硬阴影 (Hard Shadows)
表现为阴影边缘非常锋利,像刀切一样。其原因是Shadow Mapping 假设光源是一个点光源 (Point Light)。而在现实中光源(如太阳)是有体积的,会产生 本影 (Umbra) 和 半影 (Penumbra),从而形成边缘柔和的软阴影(Soft Shadows)。Shadow Mapping 原生做不到这一点。
分辨率依赖 (Resolution / Aliasing)
如果你离阴影很近,会看到阴影边缘有锯齿(马赛克)。shadow Map 本质上是一张图片(位图)。如果这张图的分辨率不够高,放大后自然会有像素感。这被称为图像空间算法的通病 。
浮点精度问题 (Z-fighting / Bias)
有时候受光面会莫名其妙出现一些黑色的斑点(脏脏的感觉)。因为我们在对比距离时,是在比较浮点数。由于计算机精度的误差,或者采样位置的微小偏差,导致“实际距离”和“记录距离”虽然理论上相等,但数值上略有差异(例如 $10.00001 > 10.00000$),导致系统误判为阴影。实际使用的过程中通常需要引入一个容差值(Tolerance 或 Bias),允许一点点误差。
光线追踪
为什么要引入光线追踪? (Why Ray Tracing?)

在之前的课程中,我们一直在学光栅化(Rasterization)。它很快,是实时渲染(如游戏)的霸主,但它有一个致命弱点:它太“局限”了。
Tip 实际上在算力极大提升的2025年,光栅化主要占据的生态位是移动端游戏和低性能PC端或主机端。
- 光栅化的局限:它在处理全局效果时非常笨拙。例如,想要画出完美的软阴影(Soft Shadows)、光泽反射(Glossy Reflection)或者间接光照(Indirect Illumination,光线弹射多次),光栅化需要各种复杂的 hack 技巧 。
- 光线追踪的优势:它符合物理直觉,能生成极其逼真的图像(如《疯狂动物城》),代价就是慢 。

光线追踪基础算法
光线投射 (Ray Casting) —— 光线追踪的雏形
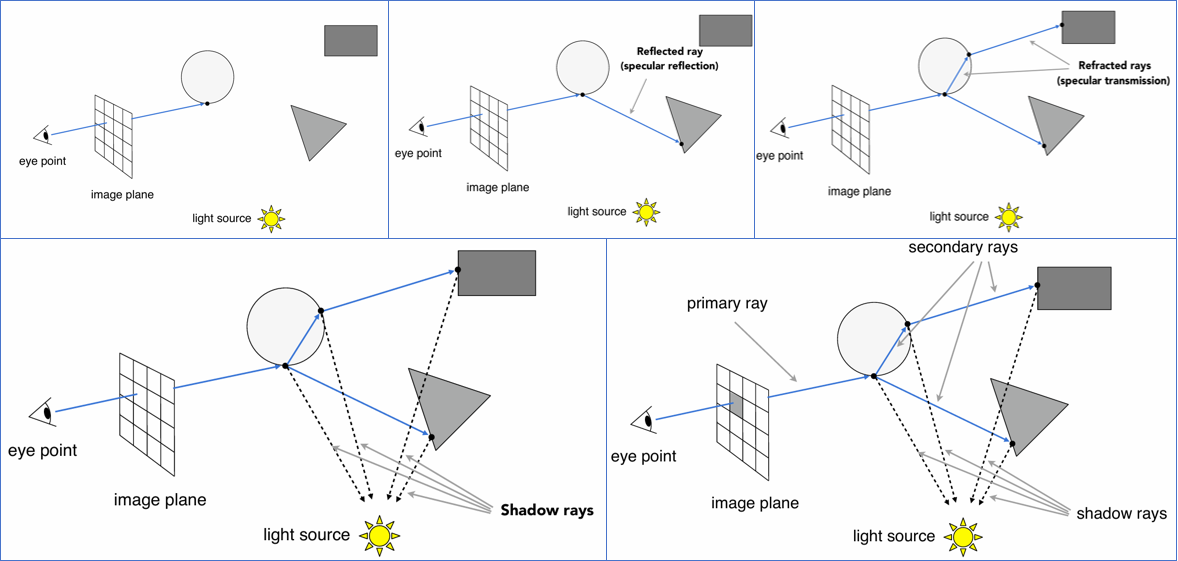
这是最早期的光线追踪算法(Appel 1968),它的核心思想基于光路可逆性:与其从光源发出亿万条光线去碰运气看哪条进入眼睛,不如从眼睛发出光线去逆向追踪光路 。

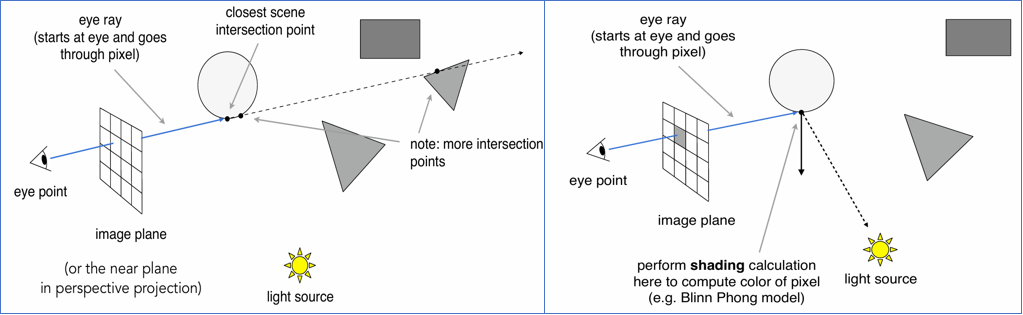
生成光线 (Generation): 假设摄像机是一个针孔相机,我们将眼睛作为起点,通过成像平面上的每一个像素 (Pixel) 发射一条射线,这条射线叫 Eye Ray 。
求交 (Intersection): 计算这条光线与场景中所有物体的交点,并找到距离眼睛最近的那个交点(因为远的会被近的挡住) 。
着色与阴影 (Shading & Shadow): 在最近的交点处,我们需要计算颜色。
- 判定阴影:从该交点向光源发射一条射线(Shadow Ray)。如果这条射线中间没有被其他物体阻挡,说明该点能被照亮;如果被阻挡,则该点处于阴影中 。
- 计算颜色:结合材质属性(如法线方向)和光照模型(如 Blinn-Phong),算出该像素的颜色 。
Whitted-Style 光线追踪 (Recursive Ray Tracing) —— 让光线“弹”起来
Ray Casting 只考虑了光线直接击中物体的效果,而 1980 年提出的 Whitted-Style 光线追踪引入了递归 (Recursion),让光线可以在物体之间反弹,从而模拟反射和折射 。
主光线 (Primary Ray): 和 Ray Casting 一样,从眼睛发出光线,找到最近的交点 。
次级光线 (Secondary Rays): 在这个交点处,根据物体的材质,光线会发生分支:
- 反射光线 (Reflection Ray):如果是镜面,光线会发生镜面反射 。
- 折射光线 (Refraction Ray):如果是玻璃或水,光线会发生折射(透射) 。
- 阴影光线 (Shadow Ray):依然需要向光源发射光线来检测阴影 。
递归计算: 反射和折射出去的新光线,会继续向前飞行,撞击下一个物体,再次产生新的反射/折射光线。这个过程会一直递归下去(直到达到设定的最大深度或光线能量衰减到忽略不计)。
颜色叠加: 最终像素的颜色 = 本色 + 反射回来的颜色 + 折射回来的颜色。
光线与表面求交 (Ray-Surface Intersection) —— 数学基础
为了实现上述算法,计算机必须能算出“光线在哪里撞到了物体”。这需要解数学方程。
1. 光线方程 (Ray Equation)
首先,我们需要用数学语言描述“光线”是什么。 在图形学中,光线被定义为从一点发出的射线。我们在数学上将光线定义为一条射线,由起点 (Origin, $o$) 和方向 (Direction, $d$) 决定。任意时刻 $t$ 的位置为:
$$ r(t) = o + t d \quad (0 \le t < \infty) $$- $r(t)$:光线在 t 时刻到达的位置。
- $t$:可以理解为“时间”或者“距离”
约束:$0 \le t < \infty$ 。
- $t=0$ 时,光线在起点 $o$。
- $t$ 必须是正数,因为光线只向前跑,不会向后跑。
2. 隐式表面求交 (Implicit Surfaces)
隐式曲面是用数学方程 $f(p)=0$ 定义的表面,以球体为例,球的方程是 $(p-c)^2 - R^2 = 0$($p$是球上一点,$c$是球心,$R$是半径)。
求交逻辑:如果光线上的某个点 $r(t)$ 也在球上,那么把光线方程代入球的方程必须成立。
$$ (o + td - c)^2 - R^2 = 0 $$求解:
这个方程展开后,本质上是一个关于未知数 $t$ 的一元二次方程 ($at^2 + bt + c = 0$) 。
- 利用求根公式 $t=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$ 求解 。
- 判定:
- 如果有两个实根,说明穿过球体(两个交点)。
- 如果有一个实根,说明相切。
- 无实根,说明没打中。
- 注意:我们需要找到最小的正实数解 $t$,这才是光线接触到的第一个点。
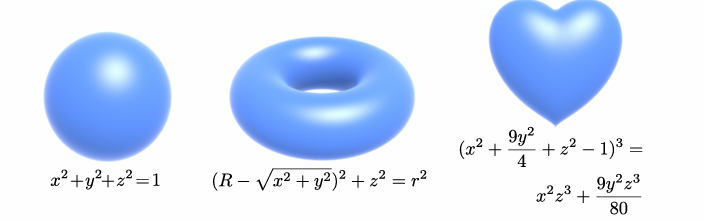
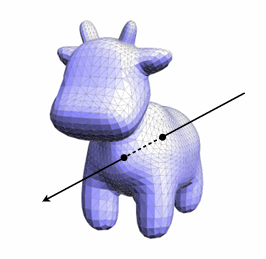
3. 显式表面求交 (Triangle Mesh)
这是图形学中最重要的情况,因为绝大多数模型(如牛、建筑、角色)都是由三角形组成的
思路一:笨办法 (Ray-Plane Intersection)
把三角形视为无限大平面的一个子集。
- 第一步:求光线与三角形所在的无限大平面的交点 。
- 平面方程定义为:$(p - p') \cdot N = 0$,其中 $N$ 是法线,$p'$ 是平面上任意一点 。
- 代入光线方程求解 $t$:$t = \frac{(p' - o) \cdot N}{d \cdot N}$ 。
- 第二步:判断这个交点是否在三角形内部 。
- 这通常利用叉积(Cross Product)来判断点是否在三条边的同一侧。
思路二:Möller-Trumbore 算法 (工业界标准)
这是一种更快速、更直接的方法,不需要先算平面交点 。
核心思想是:利用重心坐标 (Barycentric Coordinates)。
三角形内的任意一点 $P$ 可以表示为三个顶点的加权和:
$$ P = (1 - b_1 - b_2)P_0 + b_1 P_1 + b_2 P_2 $$且满足 $b_1 \ge 0, b_2 \ge 0, 1-b_1-b_2 \ge 0$ 。
联立方程,让光线上的点等于三角形内的点:
$$ O + tD = (1 - b_1 - b_2)P_0 + b_1 P_1 + b_2 P_2 $$求解:这是一个包含三个未知数 ($t, b_1, b_2$) 的线性方程组。利用克莱姆法则 (Cramer’s Rule) 可以直接推导出求解公式 。
判定:如果算出的 $t > 0$ 且 $b_1, b_2$ 符合重心坐标的范围约束,则判定为相交。
光线追踪计算加速
光线追踪的瓶颈在于,对于场景中的每一根光线,都要判断它是否与场景中的所有三角形相交。如果不加干预,复杂度是线性的 $O(N)$。加速结构的目标是构建一种层级化的数据结构,通过预处理将场景组织起来,使得光线查询的复杂度降低到对数级 $O(\log N)$ 。
想象你在图书馆找一本书(光线找三角形)。
没有加速结构:你需要从第一个书架的第一本书开始,一本一本检查书名,直到找到为止。如果有 100 万本书,你会累死。
有加速结构:你利用索引。先看“区号”(包围盒),发现书不在A区,那A区里的一万本书直接不用看了。这就是AABB 测试,快速排除无关区域。

光线与包围盒求交 (Bounding Volumes / AABB)
为了加速光线追踪,我们需要先判断光线是否碰到轴对齐包围盒 (AABB)。这一步的数学推导非常巧妙。
理解 AABB (Slabs Method)
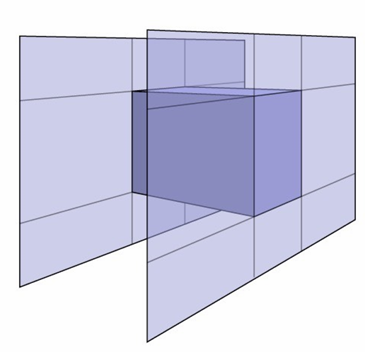
AABB 可以被理解为三对无限大的板子 (Slabs) 的交集 。
- 一对垂直于 x 轴的板子(形成了 x 轴范围 $x_{min}, x_{max}$)。
- 一对垂直于 y 轴的板子。
- 一对垂直于 z 轴的板子。
光线进入与离开:
光线 $r(t) = o + td$ 穿过一对板子(例如 x 轴方向)时,会有两个时刻:
- $t_{min} = (x_{min} - o_x) / d_x$
- $t_{max} = (x_{max} - o_x) / d_x$
- 注意:如果 $d_x$ 是负数,需要交换 $t_{min}$ 和 $t_{max}$ 确保小的值在前 。
核心求交逻辑
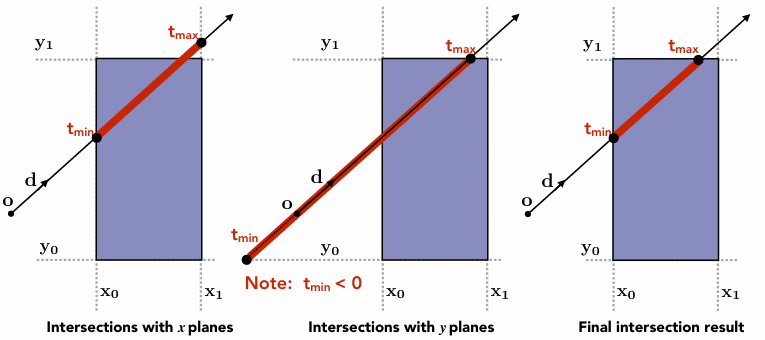
对于三维盒子,光线必须都处于三对板子中间,才算在盒子里 。
进入时间 ($t_{enter}$):光线必须进入了所有三对板子,才算真正进入盒子。就像木桶效应的反面,必须等最晚的那个。
$$ t_{enter} = \max(t_{min\_x}, t_{min\_y}, t_{min\_z}) $$离开时间 ($t_{exit}$):光线只要离开了任意一对板子,就算离开了盒子。
$$ t_{exit} = \min(t_{max\_x}, t_{max\_y}, t_{max\_z}) $$
Tip 简单来说这里就是,在三对两两对应的板子中,取出进入最晚、出去最早的值。
最终判定条件
光线与 AABB 相交,当且仅当满足以下数学条件 :
$$t_{enter} < t_{exit} \quad \text{且} \quad t_{exit} \ge 0$$- $t_{enter} < t_{exit}$:表示光线在盒子里待了一段时间(如果进入时间比离开时间还晚,说明没进去过)。
- $t_{exit} \ge 0$:表示盒子不在光线的正后方(即使光线反向延长线穿过盒子,也不算相交,因为光线只向前射)。
网格优化
不管是 Whitted-style 还是后续的 Path Tracing,如果不加优化,我们需要把每一根光线和场景里所有的三角形都做一遍求交测试 。 想象一下,如果场景里有 1000 万个三角形,一根光线就要算 1000 万次,这根本不可能实时渲染,为了解决这个问题,图形学中提出了一些加速方法。
上述方法中我们已经掌握了如何快速判断光线是否击中一个包围盒(AABB),现在将上节课学习的**原子操作(AABB 求交)整合进宏观架构(加速结构)**中。
均匀网格 (Uniform Grids)
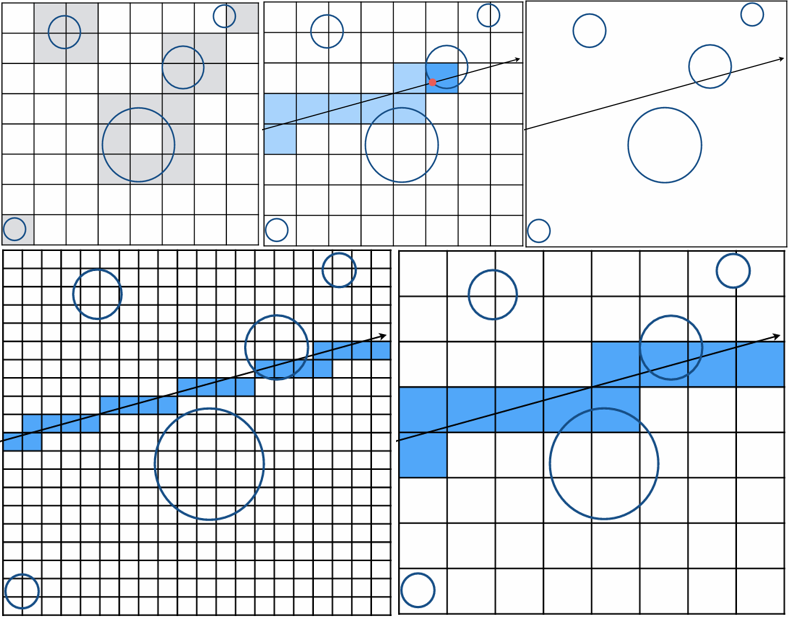
在预处理阶段,找到场景的包围盒,将其划分为分辨率相同的、规则的网格单元(Cells)。每个单元格内存储了与该单元格重叠的物体引用。光线追踪时,光线按照 3D DDA 算法(类似画直线的算法)依序遍历其穿过的网格 。

如果场景里的物体分布很均匀(比如这满屏幕的草地),这招快得飞起 。

然而对于经典的**“体育场里的茶壶” (Teapot in a stadium)** 问题。如果场景极其空旷,只有中间放个茶壶,光线会在空气中空转几万次格子检测才能碰到茶壶,效率极低 。
空间划分:KD-Tree (Spatial Partitions)
为了解决“格子太死板”的问题,我们引入了自适应的划分。
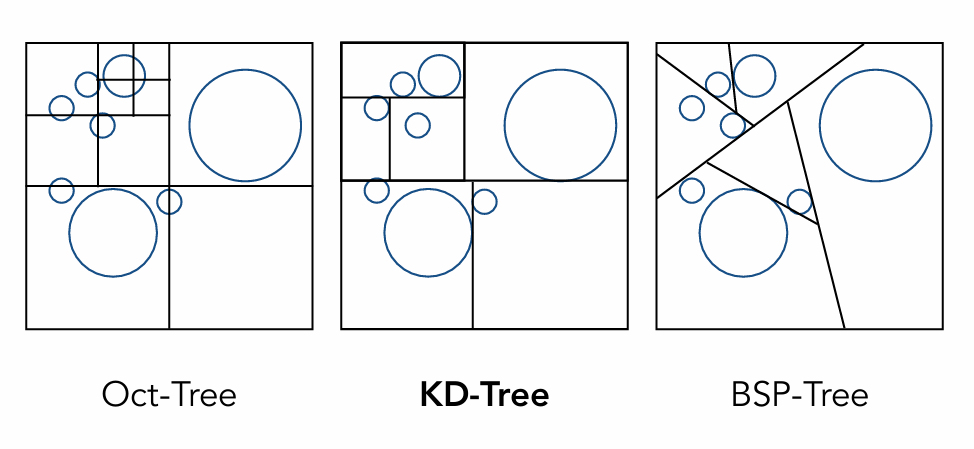
KD-Tree 是一种将空间递归二分的树形结构。
- 划分方式:交替沿着 x、y、z 轴,将当前的空间(节点)一分为二。
- 存储规则:中间节点只存“我在哪里切了一刀”(划分轴和位置),叶子节点才存储具体的物体列表 。
- 性质:子空间之间是互不重叠的(Disjoint)。
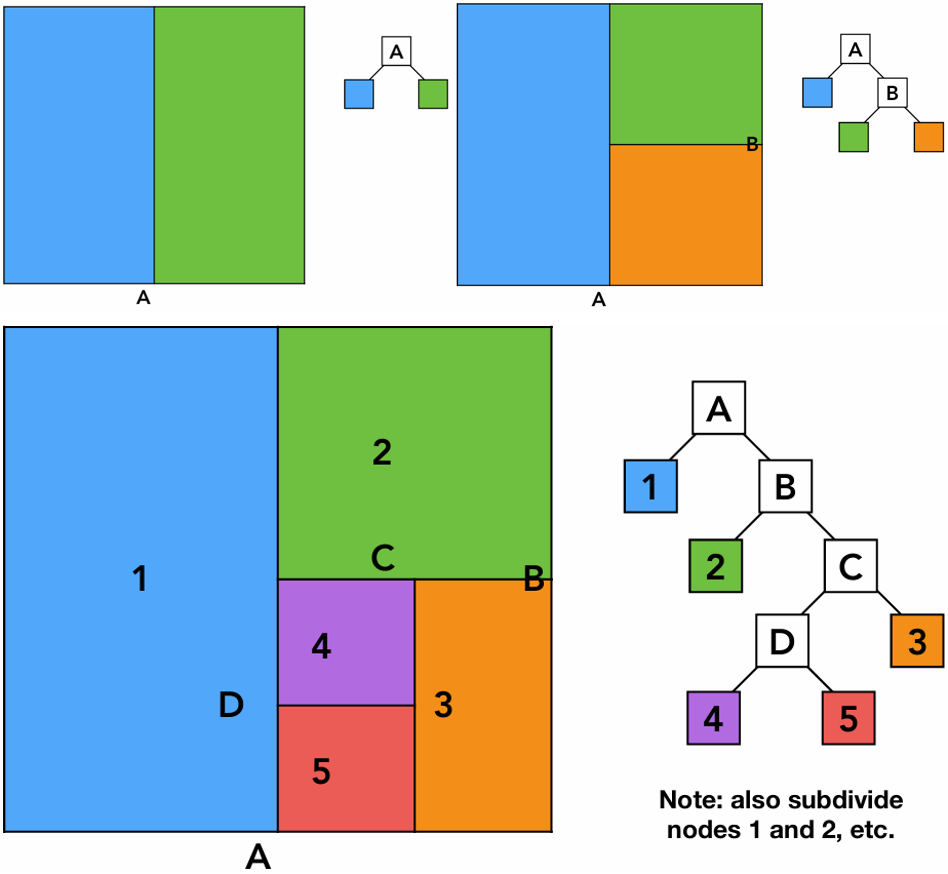
“切蛋糕”策略。切分:看着整个房间,物体哪里密,就在哪里多切几刀。比如桌子上东西多,就在桌子周围疯狂切分空间;天花板没东西,就留一大块空间。寻路:光线射进来,利用上节课学的 $t_{enter}/t_{exit}$,判断它是先穿过“左半边蛋糕”还是“右半边蛋糕”。
“被切坏的三角形”。 因为你切的是空间(蛋糕),如果有一把刀刚好切在了桌子中间,桌子(物体)就被切成了两半。 这导致同一个物体必须在“左边空间”的名单里写一次,又在“右边空间”的名单里写一次。这让数据维护变得非常恶心 。
物体划分:BVH (Object Partitions) —— 工业界主流
为了不把物体切坏,我们换一种思路:不切空间,而是分组。
Bounding Volume Hierarchy (BVH) 是基于对象的划分。
划分方式:将物体集合划分为两个子集,然后为每个子集重新计算一个紧凑的 AABB 包围盒。
性质:一个物体只属于一个节点,但不同节点的包围盒在空间上允许重叠 。
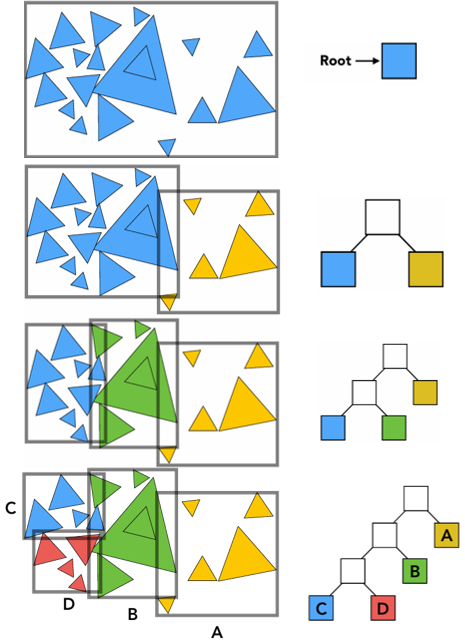
Tip 【通俗理解】
“收纳箱”策略。 既然切蛋糕会切坏东西,那我们改用收纳。
- 分组:把房间里的东西分成两堆。一堆是“家具”,一堆是“散落的玩具”。
- 打包:给“家具”套一个大箱子(AABB),给“玩具”套一个小箱子(AABB)。
- 特点:家具箱子和玩具箱子可能会堆叠在一起(空间重叠),但这没关系!关键是一个玩具绝对不会同时在两个箱子里(物体完整)。
| 策略 | 比喻 | 核心特点 | (tenter/texit) 用在哪? |
|---|---|---|---|
| 均匀网格 | 跳房子 | 空间等分,容易在空地空转 | 每进一个新格子,判断是否击中格子范围 |
| KD-Tree | 切蛋糕 | 空间二分,物体会被切碎 | 判断光线先进入切分面的左边还是右边 |
| BVH (主流) | 收纳箱 | 物体分组,箱子可重叠 | 这是核心!没击中箱子就不开箱,极大减少计算 |